Archive for the ‘FMFI UK’ Category
Modelovanie kriviek a plôch (3)
Prednáška sa koná vo štvrtok o 13:10 v F1-247.
Na úspešné absolvovanie predmetu je potrebné urobiť referát z článku. Nájdete ich buď nižšie alebo si ich môžete nájsť sami (v tom prípade ho doneste, aby som zistil, či je tematicky vhodný). Referát môžete mať kedykoľvek počas semestra.
Ak si vyberiete článok, dajte mi prosím vedieť (najlepšie e-mailom), čo ste si vybrali, aby som mohol informovať ostatných. Je možné, že si študujete niečo, čo je geometrickému modelovaniu príbuzné. Ak chcete referovať takúto prácu, doneste mi ju ukázať alebo mi pošlite linku. Ak potrebujete na prezentáciu notebook/projektor, dajte mi prosím vopred vedieť. Treba ho rezervovať. Referáty, ktoré sa neuskutočnia počas semestra (maximálne 4), si treba pripraviť na 16.12.2010.
Návod na referát
- Referát by nemal trvať viac ako 20 minút. (Vyskúšajte si to prosím!)
- Prezentujte hlavné idey článku ilustrované na príkladoch. Vyhýbajte sa technickým detailom. Tie si každý naštuduje sám, ak ho zaujme hlavná myšlienka. Radšej hovorte kratšie a zrozumiteľne ako naopak.
- Na konci zodpoviete otázky poslucháčov.
- V referáte nesmie chýbať:
- čo je dané, aké sú predpoklady konštrukcie, dôkazu
- čo chceme dosiahnuť, aký je výsledok konštrukcie, dôkazu
- aká je hlavná myšlienka konštrukcie, dôkazu, etc.
- aké pomocné prostriedky potrebujeme
- zhodnotenie výhod a nevýhod prezentovaného prístupu
- ako by sa podľa Vás dala práca rozšíriť, aplikovať, vylepšiť
- Prípravu na prednášku (slajdy, rozdajníky a iné) prosím doručte aspoň 2 týždne pred prednáškou (prosím v tlačenej verzii alebo v elektronickej vo formáte .ps alebo .pdf). Pošlem Vám spätnú väzbu.
Pokiaľ nerozumiete anglickým termínom alebo neviete ich slovenské ekvivalenty v uvedených článkoch, napíšte mi, o aký termín ide a kde sa v článku nachádza, pokúsim sa Vám pomôcť.
Články na referáty s menom referujúceho a počtom jeho predchodcov. Články sú linkami dostupné so zapnutým proxy serverom našej fakulty.
| Článok 1 | Viktor Major, 16.12.2010 | 6 | Článok 2 | 4 | Článok 3 | 0 | ||
| Článok 4 | 0 | Článok 5 | 0 | Článok 6 | 0 | |||
| Článok 7 | 0 | Článok 8 | 1 | Článok 9 | 0 | |||
| Článok 10 | 1 | Článok 11 | Júlia Kučerová, 11.11.2010 | 6 | Článok 12 | Peter Zabudlý, 18.11.2010 | 6 | |
| Článok 13 | 2 | Článok 14 | 0 | Článok 15 | 0 | |||
| Článok 16 | 0 | Článok 17 | 0 | Článok 18 | 0 | |||
| Článok 19 | 3 | Článok 20 | 5 | Článok 21 | Silvia Makúchová, 16.12.2010 | 0 | ||
| Článok 22 | 0 | Článok 23 | 0 | Článok 24 | 0 | |||
| Článok 25 | 0 | Článok 26 | 0 | Článok 27 | Matej Hudák, 9.12.2010 | 0 | ||
| Článok 28 | Szabolcs Horváth, 16.12.2010 | 7 | Článok 29 | Veronika Palkovičová, 16.12.2010 | 2 | Článok 30 | Martin Miškov, 16.12.2010 | 6 |
| Článok 31 | 0 | Článok 32 | Andrej Slašťan, 16.12.2010 | 0 | Článok 33 | 0 | ||
| Článok 34 | 0 | Článok 35 | Gábor Kiss, 2.12.2010 | 0 | Článok 36 | 0 | ||
| Článok 37 | 0 | Článok 38 | 0 | Článok 39 | 0 | |||
| Článok 40 | 0 | Článok 41 | 0 | Článok 42 | 0 | |||
| Článok 43 | 0 |
Výpočtová geometria, zimný semester 2010
Prednáška sa koná v M-VI, Uto 9:50-11:20 a M-VI, Str 9:50-11:20. Pozrite si informácie o učebnom texte. Počas semestra treba vypracovať niekoľko cvičení alebo alternatívne písomku na konci semestra. Rozsah a spôsob vypracovania je na Vás. Bližšie informácie nájdete v súbore cvicenia zo ZGA. Zadania bez riešení stiahnete tu. A tu je príklad vypracovaného cvičenia.
V nasledujúcej tabuľke je bodový zisk za riešenie úloh.
| Meno | Príklad | Riešenie | Publikovanie | Bonus | Poznámka |
|---|---|---|---|---|---|
| Ján Dzurec | P1 | 15% | |||
| P2 | 0% | ||||
| P3 | 15% | ||||
| P4 | 5% | ||||
| Szabolcs Horváth | P1 | 0% | |||
| P2 | 24% | ||||
| P3 | 0% | ||||
| P4 | 7% | ||||
| OP1 | 25% | ||||
| OP2 | 25% | ||||
| OP3 | 25% | ||||
| OP4 | 15 % | ||||
| Matej Hudák | 2.4 | 1 | |||
| 2.5 | 30 | 30 | 10 | ||
| 3.5 | 1 | ||||
| 3.9 | 15 | ||||
| 3.16 | 0 | ||||
| 4.3 | 30 | 30 | 10 | ||
| 4.6 | 10 | ||||
| 4.8 | 20 | 30 | |||
| 4.9 | 10 | ||||
| 4.13 | 20 | 30 | 10 | ||
| 4.25 | 25 | 20 | 10 | ||
| 4.26 | 50 | 10 | 10 | ||
| 5.3 | 15 | ||||
| 5.12 | 15 | ||||
| 5.20 | 15 | ||||
| 5.21 | 20 | ||||
| 6.1 | 30 | ||||
| 6.5 | 40 | ||||
| 6.6 | 10 | ||||
| 6.7 | 5 | ||||
| Gábor Kiss | 2.4 | 5 | |||
| 2.5 | 3 | ||||
| 3.2 | 20 | ||||
| 3.5 | 2 | ||||
| 3.9 | 15 | ||||
| 3.10 | 30 | ||||
| 3.11 | 15 | ||||
| 3.16 | 20 | ||||
| 3.20 | 10 | ||||
| 4.3 | 15 | ||||
| 4.6 | 45 | 30 | |||
| 4.12 | 15 | ||||
| 4.14 | 10 | ||||
| 4.15 | 10 | ||||
| 4.21 | 50 | 30 | 10 | ||
| 4.29 | 50 | 30 | 10 | ||
| vp1 | 10 | ||||
| vp2 | 0 | ||||
| vp3 | 7 | ||||
| vp4 | 30 | 20 | 20 | ||
| 5.3 | 10 | ||||
| 5.4 | 1 | ||||
| 5.5 | 5 | ||||
| 5.6 | 20 | ||||
| 5.10 | 2 | ||||
| 5.16 | 10 | ||||
| 6.1 | 0 | ||||
| 6.2 | 10 | ||||
| 6.3 | 0 | ||||
| 6.5 | 50 | 30 | 10 | ||
| 6.7 | 15 | ||||
| 6.12 | 5 | ||||
| Júlia Kučerová | 2.4 | 5 | |||
| 2.5 | 3 | ||||
| 3.2 | 20 | ||||
| 3.10 | 35 | 20 | |||
| 3.11 | 15 | ||||
| 3.16 | 0 | ||||
| 3.20 | 10 | ||||
| 4.3 | 7 | ||||
| 4.6 | 50 | 20 | 20 | ||
| 4.8 | 5 | ||||
| 4.8 | 18 | ||||
| 4.9 | 35 | 20 | 10 | ||
| 4.16 | 10 | ||||
| 4.18 | 30 | 20 | 10 | ||
| 4.28 | 25 | ||||
| 5.3 | 30 | 30 | 10 | ||
| 5.5 | 5 | ||||
| 5.6 | 30 | ||||
| 5.7 | 35 | 30 | 10 | ||
| 5.14 | 10 | ||||
| 5.16 | 10 | ||||
| 6.1 | 15 | ||||
| 6.2 | 30 | ||||
| 6.3 | 2 | ||||
| 6.5 | 0 | ||||
| Andrej Kurbel | P1 | 0% | |||
| P2 | 5% | ||||
| P3 | 25% | ||||
| P4 | 0% | ||||
| OP1 | 25% | ||||
| OP2 | 25% | ||||
| OP3 | 0% | ||||
| OP4 | 5% | ||||
| Viktor Major | P1 | 5% | |||
| P2 | 15% | ||||
| P3 | 24% | ||||
| P4 | 7% | ||||
| Silvia Makúchová | 2.4 | 15 | 20 | 10 | |
| 2.5 | 15 | ||||
| P1 | 15% | ||||
| P2 | 5% | ||||
| P3 | 5% | ||||
| P4 | 5% | ||||
| OP1 | 20% | ||||
| OP2 | 20% | ||||
| OP3 | 25% | ||||
| OP4 | 3% | ||||
| Veronika Palkovičová | P1 | 0% | |||
| P2 | 25% | ||||
| P3 | 25% | ||||
| P4 | 7% | ||||
| Andrej Slašťan | P1 | 5% | |||
| P2 | 0% | ||||
| P3 | 10% | ||||
| P4 | 10% | ||||
| OP1 | 20% | ||||
| OP2 | 5% | ||||
| OP3 | 15% | ||||
| OP4 | 15% | ||||
| Peter Zábudlý | 2.4 | 0 | |||
| 3.4 | 0 | ||||
| 3.16 | 0 | ||||
| P1 | 25% | ||||
| P2 | 20% | ||||
| P3 | 10% | ||||
| P4 | 20% |
Stiahnite si vybrané kapitoly z konvexnej geometrie.
Termíny skúšky: určíme na konci semestra, zapisovanie cez fakultný systém
Po dohode s kolegom Horváthom, je termín opravnej písomky v stredu 26.1.2011. Podmienky sú rovnaké.
Pozitívne hodnotené sú všetky chyby, ktoré nájdete v skriptách, a ktoré sa v čase ich ohlásenia nenachádzajú v súbore ERRATA.
Geometria 2, zimný semester 2010 (pre pedagogické kombinácie)
Prednáška sa koná v stredu o 13:10 v akváriu M-XI.
Stiahnite si text prednášky (PDF verzia) spolu so zadaniami cvičení. A tu sa nachádzajú podmienky získania skúšky.
Termíny skúšky: určíme na konci semestra , zapisovanie cez fakultný systém.
Päťuholník s piatimi pravými uhlami
 Na prvý pohľad to je poriadna hlúposť. Ale taký päťuholník existuje. A nielen päťuholník. Keď sa s nimi chceme stretnúť, musíme zmeniť prostredie, kde ich konštruujeme. Musíme opustiť svet euklidovskej geometrie a vojsť do sveta tej neeuklidovskej, v našom prípade hyperbolickej geometrie.
Na prvý pohľad to je poriadna hlúposť. Ale taký päťuholník existuje. A nielen päťuholník. Keď sa s nimi chceme stretnúť, musíme zmeniť prostredie, kde ich konštruujeme. Musíme opustiť svet euklidovskej geometrie a vojsť do sveta tej neeuklidovskej, v našom prípade hyperbolickej geometrie.
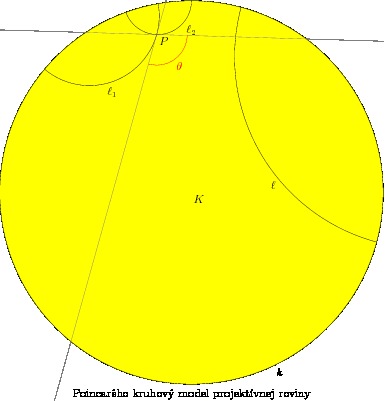
Jedným z modelov takejto roviny je Poincarého kruhový model hyperbolickej roviny. Je daný kruhom K v euklidovskej rovine (tej, na ktorú sme zvyknutý), z ktorého vynecháme hraničnú kružnicu k. Takúto množinu nazývame aj otvoreným kruhom. Bodom v takejto rovine je každý bod otvoreného kruhu. Priamky sú dvojaké. Jednak všetky priemery daného kruhu (samozrejme bez bodov ležiacich na hraničnej kružnici k) a jednak časti kružníc, ktoré sa s hraničnou kružnicou pretínajú pod pravým uhlom a ležia vo vnútri otvoreného kruhu. Uhol Θ dvoch takýchto priamok hyperbolickej roviny (teda častí euklidovských kružníc) sa určuje ako uhol dvoch euklidovských priamok, ktoré sú dotyčnicami ku kružniciam určujúcim priamky hyperbolickej roviny v ich spoločnom bode vnútri kruhu K. Asi dosť komplikované na prvý pohľad, ale obrázok všetko vyjasní.
V euklidovskej rovine sa ku každej priamke l a bodu P mimo nej dá zostrojiť jediná rovnobežka q (t.j. priamka q, ktorá nemá s tou pôvodnou spoločný žiaden bod a obsahuje bod A). V neeuklidovskej geometrii to neplatí. Špeciálne v hyperbolickej rovine existuje takých priamok viac, napr. l1 ,l2.
No a teraz úloha z názvu tohoto príspevku. Zostrojte v takejto hyperbolickej rovine ľubovoľný n-uholník, kde n je prirodzené číslo väčšie ako 2. Skúste prísť na všeobecný recept, resp odôvodniť či to vôbec ide.
Úloha sa dá formulovať v reči euklidovskej geometrie. Treba zostrojiť n kružníc, ktoré sa s kružnicou k pretínajú pod pravým uhlom. Ďalej treba nájsť cyklický zoznam týchto kružníc, v ktorom sa každé dve susedné kružnice budú pretínať pod pravým uhlom v kruhu K.
Balada o vete Rolleovej
Dovolím si reprodukovať známu baladu, vzhľadom na to, že tvrdenie budem najbližšie potrebovať na prednáške. Takže na začiatok tóny svitu luny (od Debussyho pre pamätníkov) a nedeľná chvíľka poézie môže začať.
Heinrich von Boole-Karajan
Balada o vete Rolleovej
Túto vetu – závažnú, no krátku
nechal nám pán Rolle na pamiatku.
Každému z vás iste cestu skríži
(Neubrunn, Vencko: skriptá z analýzy).
V tej vete je skrytá vôňa kvetov.
Dovoľte mi zblížiť vás s tou vetou.
Predpoklady – tie su vskutku malé:
spojitosť na celom intervale
no a vnútri, vlastnosť to nie nová
funkciu f možno derivovať.
Na okrajoch potom už len stačí
ak sa “f(a)” “f(b)” rovnať ráči.
Keď už spĺňa tieto predpoklady,
funkcia f máva veľké klady
kdesi v (a,b) bod c sa už kľuje
f ` sa v céčku vynuluje.
Snáď stratíme ešte dve-tri slová
o tom, ako vetu dokazovať:
ak f žije medzi konštantami
urobte si, prosím, dôkaz sami.
No a ak je nekonštantne pestré
celkom iste nadobúda extrém.
Zvyšok úvah, nie je ich tak veľa
nechame na prácu čitateľa.
Je to iste pocta poézie,
že pán Rolle oddnes v básňach žije.
Zato, prosím, priateľ slovesnosti
neuberaj vetám na presnosti.
To, čo básnik do obrazov snuje
matematik presne sformuluje.
(Doplnené a opravené: autorom balady je Ivan Kupka.)
Topológia a funkcionálna analýza, letný semester 2010
Prednáška sa koná v VIII, Str, 8:10-9:40, XI, Štv, 9:50-11:20 Tu možno stiahnuť text prednášky (PDF verzia) spolu so zadaniami cvičení. Linky sa zrejme časom objavia aj v AIS.
Termíny skúšok: dohodneme na konci semestra a objavia sa v AIS
Michail Gromov

Čítal som nedávno článok o vynikajúcom geometrovi, nositeľovi viacerých ocenení – Michailovi Gromovovi. V tomto roku obdržal Abelovu cenu. Jeho postreh o poznaní a jeho ďalšom šírení sa mi zdá veľmi trefný. Kontrastuje s prístupom skupiny známej ako Nicolas Bourbaki, ktorá vyrástla pred a najmä po druhej svetovej vojne a stavala na formálnosti. Zrejme treba oboje. MG píše:
…this common and unfortunate fact of the lack of an adequate presentation of basic ideas and motivations of almost any mathematical theory is, probably, due to the binary nature of mathematical perception: either you have no inkling of an idea or, once you have understood it, this very idea appears so embarrassingly obvious that you feel reluctant to say it aloud; moreover, once your mind switches from the state of darkness to the light, all memory of the dark state is erased and it becomes impossible to conceive the existence of another mind for which the idea appears nonobvious...
Viac pozri v článkoch Marcela Bergera, Encounter with a Geometer Part I, Part II, Notices of AMS 47, 2000.
Steinerov bod v trojuholníku a v štvorstene
Nech ![]() je trojuholník. Ktorý bod
je trojuholník. Ktorý bod ![]() v jeho vnútri minimalizuje
v jeho vnútri minimalizuje ![]() ? Ako je to v štvorstene?
? Ako je to v štvorstene?
Divný pútnik
![]() Po dlhšom čase som sa opäť stretol s hlavolamom o pútnikovi. Je z planéty, ktorá je guľatá, ale na rozdiel od Zeme, sa vie pútnik pohybovať po celom jej povrchu. Pútnik vyrazí zo svojho domu na juh 1 km, potom na východ 1 km a na sever 1km a ocitne sa doma. Kde je jeho domov? Prezradím, že riešenie nie je jediné.
Po dlhšom čase som sa opäť stretol s hlavolamom o pútnikovi. Je z planéty, ktorá je guľatá, ale na rozdiel od Zeme, sa vie pútnik pohybovať po celom jej povrchu. Pútnik vyrazí zo svojho domu na juh 1 km, potom na východ 1 km a na sever 1km a ocitne sa doma. Kde je jeho domov? Prezradím, že riešenie nie je jediné.
Technické zdroje k písaniu odborných prác
![]() Pri písaní bakalárskych, diplomových, rigoróznych, minimových, dizertačných… prác sa s úspechom dá využiť LaTeX. A nielen v matematicky orientovaných disciplínach je výrazným prínosom ku kvalite a uľahčovaniu prípravy textu. Ako každý komplexný nástroj, vyžaduje istý čas na zvládnutie. Tento čas sa však vyplatí investovať. Základné konštrukcie a pokyny ako tvoriť takýto zdrojový text možno nájsť vo wikiknihe o LaTeXu.
Pri písaní bakalárskych, diplomových, rigoróznych, minimových, dizertačných… prác sa s úspechom dá využiť LaTeX. A nielen v matematicky orientovaných disciplínach je výrazným prínosom ku kvalite a uľahčovaniu prípravy textu. Ako každý komplexný nástroj, vyžaduje istý čas na zvládnutie. Tento čas sa však vyplatí investovať. Základné konštrukcie a pokyny ako tvoriť takýto zdrojový text možno nájsť vo wikiknihe o LaTeXu.
K písaniu treba aj dobrý editor. Existuje ich veľa, ale dobrých je len niekoľko – pozri porovnanie. Osobne používam Emacs+AucTeX
Kreslenie obrázkov je pomerne náročná časť pri písaní práce a trvá dlhšie, kým si nájdeme ten správny nástroj. Zaujímavým programom na začiatok je inkscape.