Archive for the ‘Vyučovanie’ Category
Výpočtová geometria, zimný semester 2010
Prednáška sa koná v M-VI, Uto 9:50-11:20 a M-VI, Str 9:50-11:20. Pozrite si informácie o učebnom texte. Počas semestra treba vypracovať niekoľko cvičení alebo alternatívne písomku na konci semestra. Rozsah a spôsob vypracovania je na Vás. Bližšie informácie nájdete v súbore cvicenia zo ZGA. Zadania bez riešení stiahnete tu. A tu je príklad vypracovaného cvičenia.
V nasledujúcej tabuľke je bodový zisk za riešenie úloh.
| Meno | Príklad | Riešenie | Publikovanie | Bonus | Poznámka |
|---|---|---|---|---|---|
| Ján Dzurec | P1 | 15% | |||
| P2 | 0% | ||||
| P3 | 15% | ||||
| P4 | 5% | ||||
| Szabolcs Horváth | P1 | 0% | |||
| P2 | 24% | ||||
| P3 | 0% | ||||
| P4 | 7% | ||||
| OP1 | 25% | ||||
| OP2 | 25% | ||||
| OP3 | 25% | ||||
| OP4 | 15 % | ||||
| Matej Hudák | 2.4 | 1 | |||
| 2.5 | 30 | 30 | 10 | ||
| 3.5 | 1 | ||||
| 3.9 | 15 | ||||
| 3.16 | 0 | ||||
| 4.3 | 30 | 30 | 10 | ||
| 4.6 | 10 | ||||
| 4.8 | 20 | 30 | |||
| 4.9 | 10 | ||||
| 4.13 | 20 | 30 | 10 | ||
| 4.25 | 25 | 20 | 10 | ||
| 4.26 | 50 | 10 | 10 | ||
| 5.3 | 15 | ||||
| 5.12 | 15 | ||||
| 5.20 | 15 | ||||
| 5.21 | 20 | ||||
| 6.1 | 30 | ||||
| 6.5 | 40 | ||||
| 6.6 | 10 | ||||
| 6.7 | 5 | ||||
| Gábor Kiss | 2.4 | 5 | |||
| 2.5 | 3 | ||||
| 3.2 | 20 | ||||
| 3.5 | 2 | ||||
| 3.9 | 15 | ||||
| 3.10 | 30 | ||||
| 3.11 | 15 | ||||
| 3.16 | 20 | ||||
| 3.20 | 10 | ||||
| 4.3 | 15 | ||||
| 4.6 | 45 | 30 | |||
| 4.12 | 15 | ||||
| 4.14 | 10 | ||||
| 4.15 | 10 | ||||
| 4.21 | 50 | 30 | 10 | ||
| 4.29 | 50 | 30 | 10 | ||
| vp1 | 10 | ||||
| vp2 | 0 | ||||
| vp3 | 7 | ||||
| vp4 | 30 | 20 | 20 | ||
| 5.3 | 10 | ||||
| 5.4 | 1 | ||||
| 5.5 | 5 | ||||
| 5.6 | 20 | ||||
| 5.10 | 2 | ||||
| 5.16 | 10 | ||||
| 6.1 | 0 | ||||
| 6.2 | 10 | ||||
| 6.3 | 0 | ||||
| 6.5 | 50 | 30 | 10 | ||
| 6.7 | 15 | ||||
| 6.12 | 5 | ||||
| Júlia Kučerová | 2.4 | 5 | |||
| 2.5 | 3 | ||||
| 3.2 | 20 | ||||
| 3.10 | 35 | 20 | |||
| 3.11 | 15 | ||||
| 3.16 | 0 | ||||
| 3.20 | 10 | ||||
| 4.3 | 7 | ||||
| 4.6 | 50 | 20 | 20 | ||
| 4.8 | 5 | ||||
| 4.8 | 18 | ||||
| 4.9 | 35 | 20 | 10 | ||
| 4.16 | 10 | ||||
| 4.18 | 30 | 20 | 10 | ||
| 4.28 | 25 | ||||
| 5.3 | 30 | 30 | 10 | ||
| 5.5 | 5 | ||||
| 5.6 | 30 | ||||
| 5.7 | 35 | 30 | 10 | ||
| 5.14 | 10 | ||||
| 5.16 | 10 | ||||
| 6.1 | 15 | ||||
| 6.2 | 30 | ||||
| 6.3 | 2 | ||||
| 6.5 | 0 | ||||
| Andrej Kurbel | P1 | 0% | |||
| P2 | 5% | ||||
| P3 | 25% | ||||
| P4 | 0% | ||||
| OP1 | 25% | ||||
| OP2 | 25% | ||||
| OP3 | 0% | ||||
| OP4 | 5% | ||||
| Viktor Major | P1 | 5% | |||
| P2 | 15% | ||||
| P3 | 24% | ||||
| P4 | 7% | ||||
| Silvia Makúchová | 2.4 | 15 | 20 | 10 | |
| 2.5 | 15 | ||||
| P1 | 15% | ||||
| P2 | 5% | ||||
| P3 | 5% | ||||
| P4 | 5% | ||||
| OP1 | 20% | ||||
| OP2 | 20% | ||||
| OP3 | 25% | ||||
| OP4 | 3% | ||||
| Veronika Palkovičová | P1 | 0% | |||
| P2 | 25% | ||||
| P3 | 25% | ||||
| P4 | 7% | ||||
| Andrej Slašťan | P1 | 5% | |||
| P2 | 0% | ||||
| P3 | 10% | ||||
| P4 | 10% | ||||
| OP1 | 20% | ||||
| OP2 | 5% | ||||
| OP3 | 15% | ||||
| OP4 | 15% | ||||
| Peter Zábudlý | 2.4 | 0 | |||
| 3.4 | 0 | ||||
| 3.16 | 0 | ||||
| P1 | 25% | ||||
| P2 | 20% | ||||
| P3 | 10% | ||||
| P4 | 20% |
Stiahnite si vybrané kapitoly z konvexnej geometrie.
Termíny skúšky: určíme na konci semestra, zapisovanie cez fakultný systém
Po dohode s kolegom Horváthom, je termín opravnej písomky v stredu 26.1.2011. Podmienky sú rovnaké.
Pozitívne hodnotené sú všetky chyby, ktoré nájdete v skriptách, a ktoré sa v čase ich ohlásenia nenachádzajú v súbore ERRATA.
Geometria 2, zimný semester 2010 (pre pedagogické kombinácie)
Prednáška sa koná v stredu o 13:10 v akváriu M-XI.
Stiahnite si text prednášky (PDF verzia) spolu so zadaniami cvičení. A tu sa nachádzajú podmienky získania skúšky.
Termíny skúšky: určíme na konci semestra , zapisovanie cez fakultný systém.
Topológia a funkcionálna analýza, letný semester 2010
Prednáška sa koná v VIII, Str, 8:10-9:40, XI, Štv, 9:50-11:20 Tu možno stiahnuť text prednášky (PDF verzia) spolu so zadaniami cvičení. Linky sa zrejme časom objavia aj v AIS.
Termíny skúšok: dohodneme na konci semestra a objavia sa v AIS
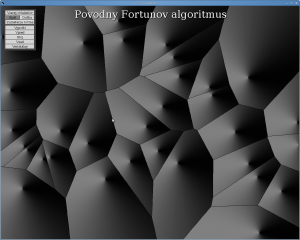
Vizualizačný nástroj algoritmov
Na prednáške Prof. Luděka Kučeru som sa dozvedel o jeho projekte AlgoVision. Je tam veľa užitočných vizualizácií bežných algoritmov na stromoch ale aj niektorých algoritmov, ktoré sa učíme na Výpočtovej geometrii. Jeho kniha je vraj dostupná vo fakultnej knižnici, v elektronickej verzii je na jeho stránke.
Modelovanie kriviek pre CAGD, letný semester 2009
Prednáška sa koná v XI, Štv, 14:50-16:20. Učebný text k prednáške je v štádiu prípravy. Jeden exemplár pracovnej verzie dám k dispozícii na prednáške.
Termíny skúšok: elektronicky systém FMFI Začíname o 9:00 pred M158. Ku skúške treba mať hodnotenie z cvičenia.
Topológia a funkcionálna analýza, letný semester 2009
Prednáška sa koná v XI, Str, 8:10-9:40, VIII, Štv, 9:50-11:20 Tu možno stiahnuť text prednášky (PDF verzia) spolu so zadaniami cvičení.
Termíny skúšok: elektronicky systém FMFI Začíname o 9:00 pred M158.
Témy bakalárskych prác
- Základné geometrické vlastnosti algebraických kriviek v rovine
- Ortogonálne transformácie
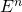
- NURBS
- T-splajny
- Minkowského priestor a jeho základné vlastnosti
- Vybrané geometrické dátové štruktúry
- Duálne čísla
- Konvexný mnohosten v
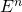
- Geometrické vlastnosti determinantu
Bližšie informácie ako aj materiály objasním pri osobnom stretnutí.
Téma diplomovej práce
Aproximácia implicitne definovanej plochy.
Práca sa zameriava na zostavenie funkčného a rozšíriteľného zdrojového kódu na aproximáciu implicitne definovaných plôch. Cieľom je vyprodukovať vzorový program s komentármi (CVS alebo podobnyý systém), ktorý bude voľne dostupný z katedrálneho servera. Práca nadväzuje na dve diplomové práce obhajované v šk. roku 2005/06 zamerané na čiastočné riešenie niektorých podproblémov.
Téma diplomovej práce
Štruktúra rovinnej a priestorovej algebraickej krivky.
Výpočet aproximácie topológie rovinnej krivky. Singulárne body, graf topológie. Topológia krivky v priestore. Zostrojiť program na výpočet a vykreslenie takýchto kriviek. Presný opis singularít na základe daných plôch ![]() a ich (lokálnych) algebraických aproximácií.
a ich (lokálnych) algebraických aproximácií.
Téma diplomovej práce
Základná diferenciálna geometria kriviek v Minkowského rovine a priestore.
Cieľom práce je študovanie modelov hyperbolickej roviny a porovnanie základných vlastností kriviek v euklidovskom a Minkowského dvojrozmernom priestore (napr. krivosť), geometrická interpretácia a vizualizácia zhodných transformácii hyperbolickej roviny. Pri rýchlom postupe sa analogické pojmy dajú študovať na krivkách v Minkowského priestore ![]() pre vhodné n ako aj zhodnosti v tomto priestore.
pre vhodné n ako aj zhodnosti v tomto priestore.