Päťuholník s piatimi pravými uhlami
Na prvý pohľad to je poriadna hlúposť. Ale taký päťuholník existuje. A nielen päťuholník. Keď sa s nimi chceme stretnúť, musíme zmeniť prostredie, kde ich konštruujeme. Musíme opustiť svet euklidovskej geometrie a vojsť do sveta tej neeuklidovskej, v našom prípade hyperbolickej geometrie.
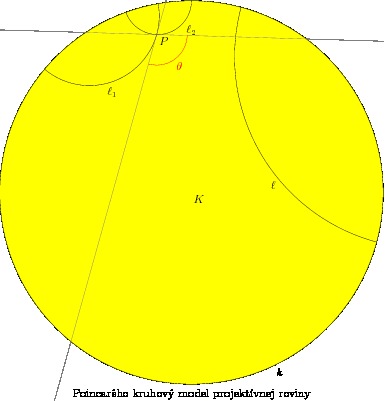
Jedným z modelov takejto roviny je Poincarého kruhový model hyperbolickej roviny. Je daný kruhom K v euklidovskej rovine (tej, na ktorú sme zvyknutý), z ktorého vynecháme hraničnú kružnicu k. Takúto množinu nazývame aj otvoreným kruhom. Bodom v takejto rovine je každý bod otvoreného kruhu. Priamky sú dvojaké. Jednak všetky priemery daného kruhu (samozrejme bez bodov ležiacich na hraničnej kružnici k) a jednak časti kružníc, ktoré sa s hraničnou kružnicou pretínajú pod pravým uhlom a ležia vo vnútri otvoreného kruhu. Uhol Θ dvoch takýchto priamok hyperbolickej roviny (teda častí euklidovských kružníc) sa určuje ako uhol dvoch euklidovských priamok, ktoré sú dotyčnicami ku kružniciam určujúcim priamky hyperbolickej roviny v ich spoločnom bode vnútri kruhu K. Asi dosť komplikované na prvý pohľad, ale obrázok všetko vyjasní.
V euklidovskej rovine sa ku každej priamke l a bodu P mimo nej dá zostrojiť jediná rovnobežka q (t.j. priamka q, ktorá nemá s tou pôvodnou spoločný žiaden bod a obsahuje bod A). V neeuklidovskej geometrii to neplatí. Špeciálne v hyperbolickej rovine existuje takých priamok viac, napr. l1 ,l2.
No a teraz úloha z názvu tohoto príspevku. Zostrojte v takejto hyperbolickej rovine ľubovoľný n-uholník, kde n je prirodzené číslo väčšie ako 2. Skúste prísť na všeobecný recept, resp odôvodniť či to vôbec ide.
Úloha sa dá formulovať v reči euklidovskej geometrie. Treba zostrojiť n kružníc, ktoré sa s kružnicou k pretínajú pod pravým uhlom. Ďalej treba nájsť cyklický zoznam týchto kružníc, v ktorom sa každé dve susedné kružnice budú pretínať pod pravým uhlom v kruhu K.
