Smoleňová K.: Procedurálne modelovanie stromov. [online] http://www.sccg.sk/~smolenova/elearning/elearning.htm Bratislava: Univerzita Komenského 2010.

Obsah

1 Úvod. 8

2 Botanická reprezentácia stromov. 9

3 Procedurálne modelovanie. 10

4 Fraktálne vlastnosti rastlín. 10

4.1 Fraktálna geometria. 10

4.2 Definícia fraktálov. 10

4.3 Rastliny a fraktály. 10

5 L-systémy. 10

5.1 L-systémy a formálne jazyky. 10

5.2 Bezkontextové L-systémy (Context-free L-systems) 10

5.3 Geometrická interpretácia reťazcov. 10

5.3.1 Korytnačia grafika v rovine. 10

5.3.2 Korytnačia grafika v priestore. 10

5.4 Rozšírenia L-systémov. 10

5.4.1 Zátvorkové L-systémy (Bracketed L-systems) 10

5.4.2 Parametrické L-systémy (Parametric L-systems) 10

5.4.3 Stochastické 0L-systémy (Stochastic 0L-systems) 10

5.4.4 Kontextové L-systémy (Context-sensitive L-systems) 10

5.4.5 Časované D0L-systémy (Timed D0L-systémy) 10

5.4.6 Mapové L-systémy (Map L-systems) 10

5.4.7 Enviromentálne L-systémy (Enviromentally-sensitive L-systems) 10

5.4.8 Otvorené L-systémy (Open L-systems) 10

5.5 Aplikácie L-systémov. 10

6 Geometrická reprezentácia stromov. 10

6.1 Reprezentácia architektúry. 10

6.1.1 Modulárna štruktúra rastlín. 10

6.2 Reprezentácia geometrie. 10

6.2.1 Detailné reprezentácie. 10

7 Modelovanie stromov. 10

8 Aplikácie virtuálnych modelov rastlín. 10

1 Úvod

Stromy sú komplexné prírodné objekty, pozostávajúce z mnohých opakujúcich sa (podobných) častí. Na ich modelovanie, podobne ako aj na modelovanie iných prírodných objektov a javov, sa v počítačovej grafike používajú procedurálne metódy, ktoré umožňujú na základe relatívne malého počtu vstupných parametrov generovať na pohľad veľmi zložité objekty, a teda aj stromy (ako bohato rozkonárené štruktúry).

V práci prinášame prehľad problematiky súvisiacej s procedurálnym modelovaním stromov. Pre lepšie pochopenie biologickej podstaty stromov sme v druhej kapitole uviedli prehľad základných botanických pravidiel uplatňujúcich sa pri raste a rozkonárovaní stromov. V tretej kapitole hovoríme o procedurálnych technikách, medzi ktoré patria aj L-systémy a algoritmy na generovanie fraktálov. Fraktálne vlastnosti rastlín popisujeme v štvrtej kapitole a teóriu L-systémov v piatej kapitole. V šiestej kapitole sa venujeme geometrickej reprezentácii stromov, pričom dôkladnejšie popisujeme rôzne detailné reprezentácie ich tvaru a štruktúr, so zameraním sa na modulárnu štruktúru rastlín. Siedma kapitola konečne prináša prehľad hlavne procedurálnych, ale aj interaktívnych techník použitých na modelovanie stromov. V ôsmej kapitole je prehľad možného využitia virtuálnych modelov rastlín.

2 Botanická reprezentácia stromov

Pri modelovaní stromov (drevín) je veľmi potrebné poznať ich biologickú stavbu a funkciu. Nasledujúca botanická časť je spracovaná podľa (Vĕtvička et al., 1992, Bobák et al., 1992)

Dreviny sú rastliny celé drevnaté, drevnatejú im aj tohtoročné výhonky, ktoré v nasledujúcom roku pokračujú v raste. Sú viacročné až dlhoveké, plodia veľa ráz a ich stonky sa obyčajne rozkonárujú. Podľa vzhľadu sa rozdeľujú na stromy, drevnaté liany a kry.

Stromy sú dreviny so stonkou (nadzemný orgán, ktorý spája orgány výživy – korene a listy) rozkonárenou až v určitej výške nad zemou, takže majú dve odlišné časti, nerozkonárený kmeň, ktorý prechádza do bohato rozkonárenej koruny.

Napriek tomu, že stonka je najtvárnejší a najpremenlivejší orgán rastlinného tela, riadi sa výstavba každej koruny dreviny presnými dedičnými zákonitosťami, hoci vonkajšie ekologické vplyvy alebo patologické stavy môžu spôsobiť vážne zmeny vo vzhľade jedinca.

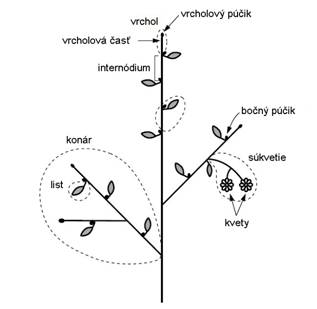
Stonka je článkovaná, rozdelená na uzly (nódy) a články (internódiá) (Obr. 2.1). Článkovanosť stonky súvisí so vznikom a pripojením listov a bočných stoniek. Uzol je miesto kde sa pripája list na stonku, kým články sú bezlisté úseky medzi dvoma nad sebou stojacimi uzlami (Bobák et al., 1992).

Obr. 2.1 Stavba stonky (upravené podľa deReffye et al., 1988).

Nové dcérske stonky (konáre) vyrastajú z púčikov materskej stonky. Púčiky sú rastové vrcholy s hrbolčekovitými základmi ďalších stoniek a listov a proti nepriaznivým poveternostným vplyvom ich obaľujú krycie šupiny. Len výnimočne sú púčiky drevín nahé (kalina siripútková) alebo polonahé (baza čierna). Púčiky sú na koncoch stoniek (vrcholové, terminálne) alebo vyrastajú na bokoch, prípadne v pazuchách listov (bočné, pazušné). Krytosemenné rastliny majú pazušný púčik takmer za každým listom, nahosemenné (ihličnaté) len pri malom počte listov. Púčiky majú nielen ochrannú funkciu a sú základmi nových stoniek, ale už z ich postavenia na stonke možno usudzovať na stratégiu obsadzovania priestoru, teda rozkonárovania. Len vďaka rozkonárovaniu môžu stromy ako dlhoveké rastliny najlepšie využiť priestor a najvhodnejšie nastaviť listy slnečným lúčom. Púčiky sú tiež dôležitým znakom pri určovaní drevín v zime, keď nemajú listy, pretože sú pre väčšinu rodov a druhov charakteristické. Na stonke sú postavené v podstate tromi spôsobmi: striedavo, protistojne a praslenovito.

Okrem týchto púčikov sa takmer všade na rastlinnom tele môžu tvoriť vedľajšie (adventívne) púčiky. Pri drevinách sú to spiace púčiky, ktoré sa prebúdzajú napríklad pri poranení stromu, alebo vytvárajú charakteristické výmladky.

Nové výhonky (konáre s listami a pazušnými púčikmi) však nevyrastajú zo všetkých založených púčikov. Tie, ktoré nevypučali sa môžu zmeniť na spiace púčiky.

Pri väčšine drevín sa vyskytujú dva základné typy konárov (Obr. 2.2), ktorých vzájomný pomer a postavenie má prvoradý vplyv na architektúru koruny.

· Predlžujúce sa bočné konáriky (makroblasty) sú dlhé výhonky s dlhotrvajúcim rastom, dlhými internódiami (článkami) a dlhými odstupmi medzi bočnými púčikmi. Tvoria sa hlavne z vrcholových a len ojedinele z bočných púčikov. Takmer všetky mladé dreviny a niektoré dreviny i v dospelosti (prútnatec, niektoré vŕby) vytvárajú len tento typ konárov.

· Skrátené bočné konáriky, konáriky obmedzeného rastu (brachyblasty) majú veľmi krátke internódiá, dlhé často len niekoľko desatín milimetra. Ich povrch je preto nápadne hrboľatý (ginko), čo spôsobujú jazvy po opadaných krycích šupinách a listové stopy. Najčastejšie majú len vrcholový púčik, z ktorého vyrastá opäť krátke internódium. Brachyblasty sú viacročné konáriky s kratšou dobou trvania (desať až pätnásť rokov) ako pri makroblaste. Sú často špecializované na určitú funkciu: nesú zväzočky ihlíc (smrekovec, céder, borovica), kvety (jabloň, hruška) alebo sú premenené na tŕne (trnka, gledíčia).

Sústava výhonkov sa všeobecne rozkonáruje podľa dvoch typov:

· Monopodiálne rozkonárovanie – vrcholový púčik zabezpečuje pokračovanie materskej stonky, z ktorej vyrastá zreteľná hlavná stonka. Na nej z bočných púčikov vyrastajú slabšie bočné stonky, ktoré nerastú v smere pôvodnej stonky a hlavnú stonku ani neprerastajú (ihličnaté dreviny).

· Sympodiálne rozkonárovanie – rast hlavnej stonky je prerušený a v jej smere vyrastá dcérska stonka, ktorá sa vytvorila z najbližšie postaveného pazušného púčika alebo dcérska stonka natoľko zosilnie, že zatlačí materskú stonku nabok a sama rastie v smere materskej stonky (dcérske stonky sú hrubšie a dlhšie ako materská stonka). Výsledné rozkonárenie vypadá navonok ako monopódium, ale hlavnú stonku tvoria v skutočnosti postupne za sebou nasledujúce stonky vyššieho stupňa (lipa, brest alebo hrab).

Na prvý pohľad sa oba typy odlíšia podľa postavenia listov a bočných konárov: zatiaľ čo pri monopódiu vyrastajú bočné stonky v pazuchách listov, pri sympódiu vyrastajú „bočné“ (v skutočnosti zatlačené hlavné) stonky proti listu (Obr. 2.2).

Obr. 2.2 Schematický nákres makroblastu, brachyblastu, monopodiálneho a sympodiálneho rozkonárovania (Vĕtvička et al., 1992) a pozdĺžnej symetrie: akrotónia, bazitónia, mezotónia (zľava doprava) (Bobák et al., 1992).

Hlavná stonka sa označuje ako stonka I. stupňa, na ktorej pri rozkonárovaní vznikajú konáre, stonky II. stupňa, rozkonárovaním ktorých sa vytvárajú stonky III. stupňa (Obr. 2.3) (Bobák et al., 1992).

Obr. 2.3 Stupeň stonky (upravené podľa deReffye et al., 1988).

Mohutnejším rozvojom konárov v rôznych výškach materského výhonku sa vytvára pozdĺžna (longitudinálna) symetria rastlín (Obr. 2.2), a to v prípade monopodiálneho aj sympodiálneho rozkonárovania. Tým rastliny ako celok nadobúdajú rozmanitý vzhľad (habitus). Rozlišujeme tri typy symetrie (Bobák et al., 1992):

· Akrotónia – bočné konáre sa v hornej časti výhonku vyvíjajú mohutnejšie (stromy).

· Bazitónia – silnejšie sa vyvíjajú konáre pri báze stonky (kry). Často sa stáva, že konáre, ktoré sa vyvinuli z bazálnych púčikov sú oveľa mohutnejšie ako hlavný výhonok a jeho vyššie konáre, alebo je hlavný výhonok vo svojom vývoji úplne potlačený.

· Mezotónia – silnejšie sa vyvíjajú stredné konáre. Tento spôsob rozkonárovania je veľmi zriedkavý.

Rozkonárenie stoniek a vzájomný pomer konárikov rozličných typov, uhol konárov a vzájomný pomer hrúbky konárov vyššieho a nižšieho stupňa určujú konečný vzhľad a textúru dreviny, prípadne jej koruny. Z hľadiska dreviny je to vždy ukážka snahy organizmu zachytiť čo najviac svetla i v mnohoposchodovej korune.

Okrem anatomických a morfologických vlastností ovplyvňujú tvar koruny do istej miery aj vonkajšie činitele, predovšetkým svetlo a vietor. Suchozemské rastliny a dreviny osobitne sú prevažne slnné. Rôzne svetelné podmienky (napríklad zatienenie alebo naopak prebytok svetla) vedú k deformácii „ideálnych“ korún: napríklad jednostranne vyklonené koruny listnatých drevín na okraji lesa alebo nad hladinou vodnej plochy, kde rastlina reaguje okrem iného aj na množstvo svetla odrazeného od hladiny. Koruna mnohých drevín vytvára zaoblenú klenutú plochu (nazýva sa solárna čiže heliodynamická), ktorá vzniká reakciou rastúcej rastliny na dopad svetelných lúčov a vytvára optimálne podmienky na využitie svetla. Ak dreviny rastú v malej skupine, reagujú na slnečné žiarenie spoločne a vytvárajú tiež spoločnú solárnu plochu, akoby išlo o jednu drevinu. Pretože efekt dopadajúceho slnečného žiarenia sa mení so zemepisnou šírkou (podľa uhla dopadu slnečných lúčov), mení sa aj klenba a uhol naklonenia solárnej plochy (s rastúcou zemepisnou šírkou rastie aj uhol naklonenia solárnej plochy smerom na slnečnú stranu, klenba je asymetrická, časť na slnečnej strane je vyvinutejšia ako časť na odvrátenej strane).

K deformácii ideálne stavanej koruny prispieva okrem svetla aj vietor (najmä vietor vanúci jedným smerom, ako napríklad na morských brehoch alebo vo vysokých horách, kde vznikajú zástavovité koruny), zatienenie stavbami alebo stromami, mechanický vplyv (konkurencia) okolitých drevín. Na stavbu a tvar koruny môže mať vplyv aj uhol svahu, na ktorom drevina rastie, štruktúra pôdy, prípadne odraz slnečných slnečných lúčov od nej.

Väčšina zmienených deformácií sa týka len osamelo rastúcich drevín. Keď drevina rastie v trvalom zápoji, reaguje príslušnou zmenou tvaru koruny najmä na konkurenciu okolostojacich drevín, pričom sa spomenuté deformačné vplyvy i vrodené vlastnosti stavby koruny stávajú druhoradými.

Korunu stromu tvorí sústava konárov, ktoré vyrastajú z kmeňa:

· Štrukturálne čiže kostrové konáre, rozhodujúce pre tvar (skelet) koruny. Sú to väčšie, hrubšie konáre, obyčajne predlžujúce sa výhonky s vegetatívnou funkciou.

· Vyplňujúce konáre, a to slabšie predlžujúce sa výhonky alebo skrátené brachyblasty, ktoré vypĺňajú korunu a majú rozhodujúce postavenie na obvode (plášti) koruny; sú to výhonky s vegetatívnou i generatívnou funkciou.

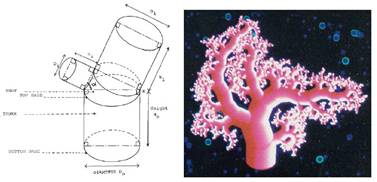
Pre jednotlivé druhy je charakteristická hustota aj tvar koruny. Ten môžeme pripodobniť ku geometrickým telesám (kužeľovitá, valcovitá, vretenovitá, valcovitá, elipsoidná, guľovitá) alebo vyjadriť pomocou špeciálnych termínov (dáždnikovitá, smútočná, zástavovitá, poschodovitá, nepravidelná) (Obr. 2.4).

Obr. 2.4 Tvar koruny: kužeľovitá, úzko vretenovitá, elipsoidná, vajcovitá, guľovitá, dáždnikovitá, nepravidelná (zľava hore) (Vĕtvička et al., 1992).

Dreviny mierneho pásma nemajú veľmi komplikovanú stavbu koruny, aj keď sa jednotlivé druhy na prvý pohľad odlišujú. Najväčší rozvoj dosiahla stavba koruny pri drevinách v tropických zemepisných šírkach. Odtiaľ čerpali Hallé, Oldeman a Tomlinson inšpiráciu pre svoj klasifikačný systém výstavby stromových korún (Hallé et al., 1978).

Východiskom boli jednoduché kritériá, ako napríklad, či výhonky sú rozkonárené (polyaxiálne dreviny) alebo nerozkonárené (monoaxiálne dreviny), či ide o monopódium alebo sympódium, či drevina rastie periodicky, rytmicky (rast prerušovaný obdobím odpočinku) alebo nepretržito (kontinuálne), či sa korene ďalej rozkonárujú, aké je postavenie súkvetí a kvetov (terminálne alebo laterálne) atď. Treba si uvedomiť, že každá z týchto vlastností vstupuje do kombinácie s ďalšími. Tak vznikla škála dvadsiatich štyroch modelov drevín (Obr. 2.5), nazývaných podľa osôb (napríklad Cookov model, Prévostov model). Aj keď ide pri tomto spracovaní architektúry drevín prevažne o tropické dreviny, niektorým modelom zodpovedajú aj dreviny mierneho pásma; napríklad rad ihličnatých drevín (Araucaria exelsa, jedle, tisy) vyhovuje Massartovmu modelu, Araucaria araucana a väčšina borovíc vrátane borovice lesnej Rauhovmu modelu, rovnako ako niektoré listnaté dreviny (javory, duby, jasene), z ďalších listnatých drevín, napríklad buky, lipy a bresty vyhovujú Trollovmu modelu.

Obr. 2.5 Architektonické modely drevín (Environmental Information Laboratory, 2007).

Dôležitým orgánom drevín sú tiež korene, ktoré sa takisto riadia určitými zákonitosťami, a vonkajšie prostredie ich deformuje podstatne výraznejšie ako napr. korunu stromu.

1 Procedurálne modelovanie

Trojrozmerný počítačový model nejakého objektu môžeme získať tromi spôsobmi (Žára et al., 2004):

1) Obrazovo-orientované modelovanie (image-based modeling) – ide o získanie trojrozmernej snímky objektu, teda hrubého modelu získaného priamo z geometrie reálneho objektu. Tú môžeme vytvoriť pomocou priestorového skeneru alebo rekonštrukciou z niekoľkých snímkov z fotoaparátu. Nevýhody sú dané veľkosťou snímaného objektu, prípadne jeho zložitosťou.

2) Interaktívne modelovanie (interactive modeling) – model vytvorí človek (animátor) za pomoci myši, klávesnice, či ďalšieho vstupného zariadenia. Tento postup je veľmi prácny, vyžaduje talent a skúsenosti, na druhej strane, výsledok je sémanticky úplne presný. Animátor totiž vie, čo robí, čo má v úmysle modelovať a čo ktorá časť modelu znamená. To je v prípade skenovania neľahké.

3) Procedurálne modelovanie (procedural modeling) – pôvodné geometrické modely (polygonálne modely, krivky, body, čiary) sú nepostačujúce na to, aby reprezentovali komplexné objekty. Preto boli vyvinuté modelovacie techniky, ktoré umožnili abstrakciu modelu, lepšiu špecifikáciu alebo vyššiu kontrolu nad modelom. Väčšina týchto techník je vo svojej podstate procedurálna. Procedurálne techniky sú časti kódu alebo algoritmy, ktoré presne určujú niektoré charakterisktiky počítačového modelu alebo efektu (Ebert et al., 1998). Model je teda získaný generovaním pomocou nejakého algoritmu. Túto metódu možno rozdeliť na dve základné podtriedy. Prvou z nich sú metódy, používané v CAD a CAGD ako napríklad šablónovanie a generovanie plôch z kriviek. Druhá podtrieda sa zameriava na automatické generovanie objektov, ktoré sa vizuálne alebo správaním podobajú objektom, s ktorými sa stretávame v prírode. Túto podtriedu môžeme rozdeliť na ďalšie skupiny:

4)  Algoritmy, ktoré vychádzajú z gramatík – napríklad L-systémy, používané najčastejšie na generovanie rastlín. Pomocou niekoľkých parametrov umožňujú simulovať zložité modely stromov, rastlín alebo iných prírodných objektov.

5)  Fraktálna geometria – algoritmy na generovanie hôr, krajín, kameňov, koralov, stromov atď.

6)  Systémy častíc – systém častíc sa reprezentuje ako veľký súbor veľmi malých prvkov (častíc), ktorých vlastnosti sa stochasticky menia v čase. Preto systémy častíc používajú veľkú databázu geometrických prvkov, ktoré reprezentujú prírodné objekty, ale animácia, pozícia, narodenie a smrť častíc sa kontrolujú algoritmicky. Patria tu algoritmy na generovanie napr. explózií, kŕdľa vtákov, padajúcich lôpt, ekosystémov, simuláciu ohňa, dymu a pod.

Výhodou procedurálnych metód je tzv. database amplification factor (Smith, 1984), ktorý umožňuje generovať a kontrolovať širokú škálu komplexných štruktúr (databázu častíc) na základe malého počtu parametrov.

2 Fraktálne vlastnosti rastlín

2.1 Fraktálna geometria

Kým umelo vytvorené predmety sa vyznačujú presnosťou geometrického opisu, popis prírodných tvarov technikami klasickej geometrie je neefektívny. Ťažko popísať mrak ako množinu gulí alebo parametrickú plochu, či modelovať krajinu ako množinu trojuholníkov. Silný a relatívne jednoduchý aparát, ktorý takéto modelovanie umožňuje, poskytuje fraktálna geometria. Na rozdiel od euklidovskej geometrie, v ktorej popisujeme objekty pomocou rovníc, vo fraktálnej geometrii sa používajú na popis objektov algoritmy, najčastejšie rekurzívne. Kým klasická geometria popisuje invariancie vzhľadom k transformáciám, ako sú otočenie či posunutie, fraktálna geometria sa zaoberá invarianciou voči zmene mierky (Žára et al., 2004). Za otca tejto vednej disciplíny sa považuje Benoit B. Mandelbrot (Peitgen et al., 1992) (Obr. 4.1).

Obr. 4.1 Mandelbrotova množina (Mandelbrot set, 2007).

2.2 Definícia fraktálov

Hlavným pojmom fraktálnej geometrie je samopodobnosť (self-similarity). Samopodobnú štruktúru môžeme rozdeliť na štruktúry, z ktorých každá je zmenšenou kópiou originálu.

Mandelbrot definoval fraktál (z lat. frangere, zlomiť) ako množinu, ktorej Hausdorff-Besicovitchova dimenzia je ostro väčšia ako topologická dimenzia 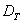(Mandelbrot, 1982). Matematicky je fraktál popísaný ako množina, ktorá vznikne zlúčením nekonečne veľa kópií samej seba (4.1) (Žára et al., 2004, str. 269):

. (4.1)

Objekty, ktoré pozorujeme v prírode, však s veľkou pravdepodobnosťou nemajú nekonečné hierarchie detailov. V zmysle rovnice sa teda nejedná o fraktály, napriek tomu sa však na základe všeobecnej dohody za fraktály považujú, aj keď presnejšie by bolo označenie fraktálom podobné. Veľkú väčšinu členitých objektov, s ktorými sa stretávame v prírode, môžeme popísať pomocou fraktálov.

2.3 Rastliny a fraktály

Aj u rastlín môžeme pozorovať samopodobnosť, čo nám umožňuje abstrakciu opakujúcich sa základných rastlinných štruktúr (modulov) a uľahčuje prácu pri pochopení stavby rastlín, ich analýze a simulácii. Niekedy sa moduly spájajú do zložitejších útvarov, v ktorých sa podobné štruktúry objavujú na rôznych úrovniach. Napríklad kvety usporiadané v zložených súkvetiach alebo viacnásobne zložené listy rastlín, ktorých lístky sú podobné celému listu (Obr. 4.2). Tieto vlastnosti využíva pri modelovaní aj Prusinkiewicz (2001).

Obr. 4.2 Ukážky samopodobnosti u rastlín.

Samopodobnosť možno pozorovať aj u stromov, napr. pri rozkonárovaní, aj keď je menej výrazná ako u bylinných druhov. Je to spôsobené tým, že ich rast trvá veľmi dlho (v porovnaní s bylinnými druhmi), a preto sú viac ovplyvnené vonkajšími vplyvmi prostredia.

Napriek tomu, že popis rastlín ako celku, zloženého z podobných častí, má veľký význam (pre ich analýzu a následné modelovanie) a vnímanie samopodobnosti u rastlín je známe už niekoľko desaťročí, doteraz neexistovalo žiadne formálne kritérium pre určenie stupňa podobnosti. Prusinkiewicz (2004b) predstavil nový pojem, topologickú samopodobnosť (topological self-similarity), ktorá je u rastlín bežnejšia ako geometrická samopodobnosť (geometric self-similarity). Geometrická samopodobnosť sa vo všeobecnosti vyjadruje ako množina afinných transformácií, ktoré zobrazujú štruktúru do jej zložiek, kým topologická sa zaoberá usporiadaním a vzťahmi medzi týmito zložkami. Formálnu definíciu samopodobnosti a jej merania, prispôsobenú na vetviace sa rastlinné štruktúry, navrhli Ferraro et al. (2005). Na jej meranie používajú algoritmus na výpočet topologických vzdialeností medzi rozkonárenými štruktúrami.

Aký je však vzťah medzi fraktálmi a rastlinami? Považovať rastliny za aproximácie „perfektných“ fraktálnych štruktúr by nebolo akceptovateľné. Životaschopnejší prístup je ten opačný, a to považovať fraktály za abstraktný popis reálnych biologických štruktúr (Prusinkiewicz et al., 1990). Môže sa zdať, že popísať list pomocou hladkej krivky je jednoduchšie ako pomocou nepravidelného obrysu fraktálu. Vysvetlenie spočíva v tom, čo znamená jednoduchšie. Intuitívne sa krivka zdá byť jednoduchšia, ale ak meriame zložitosť objektu dĺžkou najkratšieho algoritmu, ktorý ho generuje, opak je pravdou.

Fraktálny prístup k analýze rastliny, s dôrazom na samopodobnosť, ponúka kľúč k pochopeniu komplexnej stavby rastlín a ponúka rekurzívne procedúry, cez ktoré mohli byť jednotlivé štruktúry vytvorené.

3 L-systémy

V roku 1968 biológ Aristid Lindenmayer predstavil formalizmus na modelovanie a simulovanie vývoja mnohobunkových organizmov (sinice Anabaena catenula) (Obr. 5.1), neskôr nazvaný L-systémy (Lindenmayerove systémy).

L-systémy pôvodne neumožňovali modelovanie vyšších rastlín. Neskôr však bolo navrhnutých niekoľko geometrických interpretácií L-systémov, vďaka ktorým sa z nich stal univerzálny nástroj na modelovanie rastlín a boli prijaté ako matematický formalizmus pre popis vývinu rastlín (Prusinkiewicz, 1990, Prusinkiewicz et al., 1995).

3.1 L-systémy a formálne jazyky

L-systémy možno chápať ako modifikáciu formálnych jazykov, keďže ich základným konceptom je prepisovanie reťazcov (postupnosti symbolov) (string-rewriting systems) podľa určitých pravidiel. Pri tomto postupe sa zložité objekty definujú pomocou postupne sa nahrádzajúcich častí počiatočného objektu. Získaná postupnosť sa potom interpretuje geometricky. Rozdiel medzi formálnymi jazykmi a L-systémami je v spôsobe aplikácie prepisovacích pravidiel. Pri formálnych gramatikách sú pravidlá aplikované postupne, kým pri L-systémoch sú použité súbežne (paralelne). Tento rozdiel vyplýva z biologickej motivácie L-systémov (pravidlá majú zachytiť delenie buniek v mnohobunkovom organizme, kde sa súčasne delí viacero buniek naraz).

3.2 Bezkontextové L-systémy (Context-free L-systems)

Najjednoduchšiu triedu L-systémov predstavujú deterministické bezkontextové L-systémy, označované ako D0L-systémy. Formálne ich môžeme definovať takto (Prusinkiewicz, 1990):

Nech  je abeceda, je množina všetkých slov nad a je množina neprázdnych slov nad V. Reťazcový 0L-systém je usporiadaná trojica , kde:

· je abeceda systému,

· je neprázdne slovo nazývané axióma a

· je konečná množina prepisovacích pravidiel.

Prepisovacie pravidlo budeme zapisovať ako . Písmeno sa nazýva predchodca (predecessor, ľavá strana, prepisovaný symbol) a slovo sa nazýva nasledovník (successor, pravá strana) pravidla. Predpokladá sa, že pre každé písmeno existuje aspoň jedno slovo také, že . Ak nie je pre niektorý prepisovaný symbol explicitne zadané prepisovacie pravidlo, predpokladá sa, že obsahuje identické pravidlo . 0L-systém je deterministický (označenie D0L-systém), práve vtedy, keď pre každé existuje práve jedno také, že .

Nech je ľubovoľné slovo nad abecedou V. Slovo je priamo odvodené zo slova (alebo generované slovom ), označenie , práve vtedy, keď , pre všetky . Slovo je generované L-systémom deriváciou dĺžky n, ak existuje derivačná postupnosť slov taká, že , a .

Nasledujúci príklad ilustruje použitie D0L-systémov na simuláciu rastu časti mnohobunkového vlákna sinice Anabaena catenula. Symboly a reprezentujú cytologické štádium buniek (ich veľkosť a schopnosť deliť sa). Indexy a udávajú polaritu bunky, ktorá určuje pozíciu, v ktorej budú vytvorené dcérske bunky typu alebo . Vývoj je popísaný nasledujúcim L-systémom:

Začínajúc jednou bunkou (axióma) a použitím prepisovacích pravidiel až , vzniká nasledujúca postupnosť slov:

Pod mikroskopom by sme mohli filamenty (vlákna) pozorovať ako sled valcových útvarov (buniek) rôznej dĺžky, s dlhšími bunkami typu a kratšími bunkami typu (Obr. 5.1). Vzhľadom na diskrétny charakter D0L-systémov, rast buniek medzi deleniami nie je zachytený.

Obr. 5.1 Vlákno sinice a simulácia vývinu vlákna použitím D0L-systému (Prusinkiewicz et al., 1990).

3.3 Geometrická interpretácia reťazcov

V snahe použiť L-systémy na modelovanie vyšších rastlín bolo navrhnutých niekoľko grafických interpretácií L-systémov. Ich prehľad možno nájsť napr. v (Prusinkiewicz et al., 1990, s. 6). Prusinkiewicz sa zameral na interpretáciu pomocou korytnačej grafiky, známej z jazyka LOGO (Abelson et al., 1982). Základná myšlienka spočíva v tom, že reťazec symbolov vytvorený pomocou L-systému sa interpretuje ako postupnosť príkazov, ktoré kontrolujú pohyb korytnačky (Prusinkiewicz, 1986a).

3.3.1 Korytnačia grafika v rovine

Stav korytnačky (state of the turtle) je definovaný ako usporiadaná trojica , kde karteziánske súradnice reprezentujú pozíciu korytnačky a uhol jej orientáciu (smer, v ktorom sa korytnačka pohybuje dopredu). Na základe vstupných údajov, ktorými sú dĺžka kroku d a prírastok uhla , môže korytnačka odpovedať na príkazy, ktoré sú reprezentované nasledujúcimi symbolmi (Obr. 5.2):

F Pohni sa dopredu o krok dĺžky d a nakresli čiaru zo starej do novej pozície. Stav korytnačky sa zmení na , kde a .

f Pohni sa dopredu o krok dĺžky d, bez nakreslenia čiary.

+ Otoč sa doľava o uhol (proti smeru hodinových ručičiek). Stav korytnačky sa zmení na .

Otoč sa doprava o uhol (v smere hodinových ručičiek). Stav korytnačky sa zmení na .

Stav korytnačky sa zmení zakaždým, keď sa interpretuje symbol. Ak je daný reťazec , pôvodný stav korytnačky a pevné parametre d a , odpoveď korytnačky na reťazec sa interpretuje ako postupnosť korytnačkou nakreslených čiar (Obr. 5.2).

Obr. 5.2 Interpretácia symbolov , , pomocou korytnačej grafiky (Prusinkiewicz et al., 1990).

L-systémy možno použiť aj na generovanie klasických fraktálov (Prusinkiewicz et al., 1990, Peitgen et al., 1992). Napríklad všeobecne známu Kochovu vločku (Obr. 5.3) možno získať interpretáciou reťazcov vytvorených nasledujúcim L-systémom:

Obr. 5.3 Prepisovacie pravidlo p (hore), axióma ω (dole vľavo) a niekoľko prvých iterácií Kochovej vločky (Prusinkiewicz et al., 2003).

3.3.2 Korytnačia grafika v priestore

Interpretáciu L-systémov pomocou korytnačej grafiky možno rozšíriť do priestoru (Prusinkiewicz et al., 1990). Aktuálna orientácia korytnačky v priestore je daná tromi vektormi , , , ktoré označujú:

(heading) smer, v ktorom sa korytnačka pozerá dopredu,

(left) smer doľava a

(up) smer hore.

Obr. 5.4 Kontrola korytnačky v priestore (Prusinkiewicz et al., 1990).

Tieto vektory majú jednotkovú dĺžku, sú navzájom kolmé a spĺňajú rovnosť . Rotácie korytnačky možno potom vyjadriť rovnosťou , kde je rotačná matica rozmeru . Rotácie o uhol okolo vektorov , , sa reprezentujú maticami:

(5.1)

(5.2)

(5.3)

Pôvodný stav korytnačky je daný v počiatku kateziánskej súradnicovej sústavy, s vektorom v kladnom smere osi y a vektorom v zápornom smere osi x.

Orientáciu korytnačky v priestore riadime nasledujúcimi symbolmi (Obr. 5.4):

Otoč sa doľava (turn left) o uhol . Použije sa rotačná matica .

Otoč sa doprava (turn right) o uhol . Použije sa rotačná matica .

Nakloň sa dolu (pitch down) dolu o uhol . Použije sa rotačná matica .

Nakloň sa hore (pitch up) o uhol . Použije sa rotačná matica .

Nakloň sa doľava (roll left) o uhol . Použije sa rotačná matica .

Nakloň sa doprava (roll right) o uhol . Použije sa rotačná matica .

Otoč sa dookola. Použije sa rotačná matica .

Podrobnejšie spracovanú grafickú interpretáciu L-systémov pomocou korytnačej grafiky s mnohými ďalšími rozšíreniami, výrazne zlepšujúcimi realizmus modelov možno nájsť v (Mĕch et al., 2007).

3.4 Rozšírenia L-systémov

3.4.1 Zátvorkové L-systémy (Bracketed L-systems)

Podľa doteraz predstavených pravidiel korytnačka interpretuje reťazec symbolov ako postupnosť čiar. V závislosti od ich dĺžky a uhlov medzi nimi sa výsledná čiara pretína alebo nie, je viac či menej zatočená a môže mať niektoré segmenty nakreslené viackrát alebo iné mať neviditeľné, stále však ostáva iba jednoduchou čiarou. V prírode ale dominujú vetviace sa štruktúry, a preto bol, na modelovacie účely, potrebný aj matematický popis tvarov majúcich „stromovitú“ štruktúru a metódy na ich generovanie. Jedna z možností je reprezentovať rozkonárené časti ako reťazce so zátvorkami [ a ], ktoré budú vymedzovať určitý konár stromu, teda budú predstavovať jeho začiatok a koniec (Obr. 5.5).

Obr. 5.5 Príklady rozvetvených štruktúr vytvorených zátvorkovými L-systémami (Prusinkiewicz et al., 1990).

Korytnačke do funkčnosti pribudne zásobník, do ktorého bude môcť ukladať svoj stav (Prusinkiewicz et al., 1990). V korytnačej grafike sa dva nové symboly interpretujú takto:

[ Ulož do zásobníka aktuálny stav korytnačky. Do zásobníka sa uloží informácia o pozícii a orientácii korytnačky a tiež tu môžu byť údaje o iných atribútoch, napríklad o farbe a šírke kreslených čiar.

] Vyber stav korytnačky zo zásobníka a nastav ho ako aktuálny. Nenakreslí sa žiadna čiara aj keď sa pozícia korytnačky obyčajne mení.

3.4.2 Parametrické L-systémy (Parametric L-systems)

Hlavným problémom pri D0L-systémoch je, že dĺžka čiar sa redukuje na celočíselné násobky jednotkového segmentu. Okrem toho každá zmena dĺžky čiary alebo uhla otočenia by znamenala nový symbol, čo by viedlo k veľkému nárastu symbolov a prepisovacích pravidiel a špecifikácia D0L-systému by sa príliš skomplikovala. Tento problém bol vyriešený zavedením parametrických L-systémov (Prusinkiewicz et al., 1997), ktoré umožňujú doplniť jednotlivé symboly o číselné parametre (Obr. 5.6).

Parametrické L-systémy pracujú s parametrickými slovami, čo sú reťazce modulov, skladajúcich sa z písmen abecedy a k nim priradených parametrov. Písmená sú prvky abecedy a parametre sú z množiny reálnych čísel . Modul s písmenom a parametrami je označený ako . Každý modul je z množiny , kde je množina všetkých konečných postupností parametrov. Množina všetkých reťazcov modulov a množina všetkých neprázdnych reťazcov je označená ako a .

Modul má vo svojej špecifikácii formálne parametre, ktoré nadobúdajú konkrétne hodnoty (aktuálne parametre) z množiny reálnych čísel. Aktuálne parametre, ktoré sa nachádzajú v slovách, sa zhodujú s formálnymi parametrami, ktoré sú použité v prepisovacích pravidlách L-systémov. Ak je množina formálnych parametrov, potom označuje logický výraz s parametrami z a je aritmetický výraz s parametrami z tej istej množiny. Obidva typy výrazov sa skladajú z formálnych parametrov a číselných konštánt, ktoré sú kombinované použitím aritmetických operátorov , , , ; exponenciálneho operátora , relačných operátorov , , , , ; logických operátorov , , (negácia, a, alebo) a zátvorky (). Výrazy tiež môžu obsahovať volania štandardných matematických funkcií ako prirodzený logaritmus, sínus, funkcie vracajúce náhodné premenné. Symboly pre operátory a pravidlá na vytvorenie syntakticky správnych výrazov sú rovnaké ako pre programovací jazyk C. Relačné a logické výrazy nadobúdajú pre nepravdivý výrok (false) hodnotu 0, pre pravdivý výrok (true) hodnotu 1. Logické tvrdenie označené ako prázdny reťazec má hodnotu rovnú 1. Množiny všetkých správne vytvorených logických a aritmetických výrazov s parametrami z sa označujú , .

Parametrický 0L-systém je usporiadaná štvorica , kde

· je abeceda systému,

· je množina formálnych parametrov,

· je neprázdne parametrické slovo nazývané axióma,

· je konečná množina pravidiel.

Symboly a sú použité na oddelenie troch častí pravidla: prepisovaný symbol (predecessor), podmienka (condition), pravá strana pravidla (successor). Preto má pravidlo v 0L-systéme tvar

.

Číslica „0“ v názve „0L-systém“ znamená, že nezáleží na kontexte, v akom sa prepisovaný symbol nachádza.

Napríklad pravidlo s prepisovaným symbolom , podmienkou a pravou stranou je zapísané ako

.

Prepisovacie pravidlo môže byť aplikované na modul v parametrickom slove, ak sú splnené nasledujúce podmienky:

· písmeno v module je rovnaké ako písmeno v prepisovanom symbole,

· počet aktuálnych parametrov v module je rovný počtu formálnych parametrov v predchodcovi prepisovacieho pravidla a

· podmienka je pravdivá, ak sú formálne parametre v pravidle nahradené aktuálnymi parametrami.

Odvodenie je podobné ako pri bezkontextových L-systémoch.

Pri interpretácii korytnačka číta jednotlivé moduly a hodnoty ich parametrov interpretuje geometricky. Parameter môže určovať dĺžku kroku korytnačky, hrúbku čiary, ktorú nakreslí alebo uhol, o ktorý sa otočí. Ak je k symbolu priradených viac parametrov, hodnotu stavu korytnačky bude určovať prvý parameter. Ak sa za symbolom nenachádza žiadny parameter, budú použité prednastavené hodnoty, špecifikované na začiatku. Základné symboly, ktoré môžu byť ovplyvnené parametrami, sú tieto:

Pohni sa dopredu o krok dĺžky a nakresli čiaru zo starej do novej pozície. Pozícia korytnačky sa zmení na .

Pohni sa dopredu o krok dĺžky , bez nakreslenia čiary.

Otoč sa okolo o uhol stupňov. Ak je kladné, korytnačka sa otočí doľava, ak je záporné, korytnačka sa otočí doprava.

Otoč sa okolo o uhol stupňov. Ak je kladné, korytnačka sa natočí dolu, ak je záporné, korytnačka sa natočí hore.

Otoč sa okolo o uhol stupňov. Ak je kladné, korytnačka sa natočí doprava, ak je záporné, korytnačka sa natočí doľava.

Symboly , , a sa používajú ako písmená abecedy a tiež ako operátory v logických a aritmetických výrazoch, pričom ich význam závisí od kontextu.

Obr. 5.6 Príklady stromových štruktúr vytvorených parametrickým L-systémom, s rôznymi hodnotami parametrov pre uhly rozkonárovania, dĺžku a šírku konárov a pod. (Prusinkiewicz et al., 1997).

3.4.3 Stochastické 0L-systémy (Stochastic 0L-systems)

Všetky rastliny vytvorené deterministickým L-systémom sú identické. Premenlivosť, charakteristická pre biologické organizmy, môže byť dosiahnutá pridaním náhodnosti do interpretácie symbolov pomocou korytnačky, L-systému alebo oboch (Obr. 5.7). Náhodnosť (randomization) interpretácie ako samotnej má limitujúci efekt. Kým geometria (geometric aspect) rastliny, ako napríklad dĺžka stonky alebo uhly medzi vetvami, je zmenená, základná topológia ostáva nezmenená. Naopak, pridanie náhodnosti do použitia prepisovacích pravidiel, môže ovplyvniť topológiu aj geometriu rastliny (Prusinkiewicz et al., 1990).

Parametrický stochastický 0L-systém je usporiadaná pätica (Prusinkiewicz et al., 1997). Abeceda V, množina formálnych parametrov , axióma a množina prepisovacích pravidiel P sa definujú ako pri parametrických D0L-systémoch. Funkcia určuje aritmetický výraz vracajúci nezáporné číslo, nazývané pravdepodobnostný faktor (probability factor) pre každé prepisovacie pravidlo . Pravidlo v stochastickom L-systéme bude mať tvar

,

kde pred, cond a succ majú taký istý význam ako v parametrických L-systémoch a prob je výraz vracajúci pravdepodobnostný faktor.

Ak je množina prepisovacích pravidiel, ktoré možno aplikovať na daný modul v prepisovanom reťazci, potom pravdepodobnosť použitia príslušného pravidla na tento modul je rovná:

. (5.4)

Vo všeobecnosti táto pravdepodobnosť nie je konštanta priradená k pravidlu, ale závisí od hodnôt parametra v prepisovanom module.

Odvodenie budeme nazývať stochastická derivácia v , ak pre každý výskyt modulu v slove je pravdepodobnosť aplikácie pravidla s prepisovaným symbolom daná rovnicou (5.4)

Podľa tejto definície, v jednom derivačnom kroku môžu byť použité rôzne pravidlá s rovnakou ľavou stranou na rovnaký modul, vyskytujúci sa na rôznych miestach.

Obr. 5.7 Príklady stromových štruktúr vytvorených stochastickým L-systémom (Prusinkiewicz et al., 1994).

3.4.4 Kontextové L-systémy (Context-sensitive L-systems)

Pravidlá v 0L-systémoch sú bezkontextové, t. j. sú použité bez ohľadu na to, v akom kontexte sa nachádza prepisovaný symbol. Aplikácia pravidla závislého od kontextu umožňuje simulovať interakcie medzi jednotlivými časťami rastliny a šírenie látok (živín, hormónov) vo vnútri rastliny.

Kontextové L-systémy môžeme podľa tvaru pravidiel rozdeliť do niekoľkých tried (Prusinkiewicz et al., 1990).

2L-systémy používajú pravidlá v tvare , kde symbol (strict predecessor) môže byť nahradený pravou stranou vtedy a len vtedy, ak mu predchádza symbol a nasleduje ho symbol . Symboly a tvoria ľavý a pravý kontext symbolu v tomto pravidle. Pravidlo v kontextovom L-systéme možno zapísať nasledovne:

,

kde pred, cond a succ majú taký istý význam ako v parametrických L-systémoch, lc a rc sú ľavý (left context) a pravý kontext (right context).

Pravidlá v 1L-systémoch majú len ľavý alebo len pravý kontext, teda sú tvaru alebo .

0L-systémy, 1L-systémy a 2L-systémy patria do širšej triedy IL-systémov, tiež nazývaných (k,l)-systémy. V (k,l)-systémoch je ľavý kontext slovo dĺžky  a pravý kontext je slovo dĺžky .

3.4.5 Časované D0L-systémy (Timed D0L-systémy)

Pôvodný formalizmus L-systémov poskytuje model vývinu, ktorý je diskrétny v čase aj priestore. Diskretizácia v čase znamená, že stav modelu je známy iba v presných časových intervaloch. Diskretizácia v priestore znamená, že rozsah stavov modelu je limitovaný na konečný počet. Tomuto sa dá vyhnúť použitím parametrických L-systémov, modely sú však aj napriek tomu stále známe iba v diskrétnych časových intervaloch. Toto predstavuje problém pri animáciách, kde sa vyžaduje plynulý sled vývinových foriem. Vývin prebiehajúci v spojitom čase možno vyjadriť použitím formalizmu časovaných D0L-systémov (Prusinkiewicz et al., 1990). Základný rozdiel medzi týmto a predchádzajúcimi typmi L-systémov spočíva v definícii dĺžky derivácie. Kým u „obyčajných“ L-systémov sa vyjadruje ako počet derivačných krokov, u časovaných L-systémov predstavuje celkový uplynutý čas od začiatku pozorovania (derivačného procesu).

3.4.6 Mapové L-systémy (Map L-systems)

Veľa štruktúr v prírode má zložitú topológiu, ktorú nemožno popísať pomocou doterajších rozšírení (formalizmu) L-systémov. Medzi ne patria jednovrstvové (mikroskopické) bunkové štruktúry, napr. papradie gametofyty (štádium životného cyklu, v ktorom sa tvoria pohlavné bunky, pohlavná generácia), živočíšne embryá, rastlinná pokožka (Obr. 5.8). Z matematického pohľadu ich možno reprezentovať pomocou rovinných grafov s cyklami, nazývaných mapy (maps). Mapa je konečná množina regiónov (regions), kde každý región je obklopený hranicou, ktorá pozostáva z konečnej, kruhovej postupnosti hrán (edges), stretávajúcich sa vo vrcholoch (vertices). Pre hrany a vrcholy platia určité pravidlá (Nakamura et al., 1986).

Obr. 5.8 Simulovaný vývoj a fotografia gametofytu druhu Microsorium linguaeforme (Prusinkiewicz et al., 1990).

Mapy sa zhodujú s mikroskopickým pohľadom na vrstvu buniek. Regióny reprezentujú bunky a hrany bunkové steny, kolmé na rovinu pohľadu.

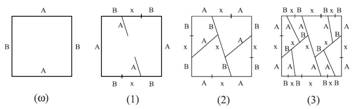
Na popis a simuláciu vývinu týchto bunkových štruktúr slúži nová trieda, mapové L-systémy (Prusinkiewicz et al., 1990) (Obr. 5.9). Mapový 0L-systém je prepisovací systém, ktorý nepracuje nad reťazcami symbolov, ale nad mapami, pričom neumožňuje interakciu medzi regiónmi. Región sa môže rozdeliť na najviac dva dcérske regióny, hrany nemožno zrušiť, čo znamená, že regióny (bunky) nemôžu splynúť ani zaniknúť.

Obr. 5.9 Príklad mapového L-systému (Prusinkiewicz et al., 1990).

3.4.7 Enviromentálne L-systémy (Enviromentally-sensitive L-systems)

Rast rastliny ovplyvňujú vnútorné (endogénne), ale aj vonkajšie (exogénne) faktory. Pôsobenie vnútorných faktorov (prenos genetickej informácie, šírenie hormónov, živín a vody) možno simulovať pomocou kontextových L-systémov. Na simuláciu vplyvu vonkajších podmienok (vplyv svetla, prítomnosť mechanických prekážok) bolo navrhnutých niekoľko techník, žiadna z nich však neumožňovala kombinovať súčasne vplyv endogénnych aj exogénnych faktorov. Pritom v prírode je takáto kombinácia zjavná, napríklad pri odpovedi rastliny na prítomnosť alebo neprítomnosť svetla, pri stretnutí sa s prekážkou, prerezávaní resp. orezaní konárov (Obr. 5.10) alebo pri reakcii na napadnutie hmyzom.

Obr. 5.10 Odpoveď stromu na orezávanie (malé krúžky predstavujú spiace púčiky, veľké naznačujú pozíciu šíreného signálu) a model záhrady (Prusinkiewicz et al., 1994).

Ako riešenie tohto problému boli predstavené enviromentálne L-systémy (Prusinkiewicz et al., 1994). Generovaný reťazec sa interpretuje po každom derivačnom kroku a hodnoty korytnačky sa vrátia ako parametre pre vyhradené moduly (query modules) v reťazci. Každý derivačný krok prebieha ako v parametrických L-systémoch s tým, že na rozdiel od nich, v enviromentálnych L-systémoch zostávajú parametre spojené s modulmi (query modules) nedefinované. Počas grafickej interpretácie je týmto modulom priradená hodnota v závislosti od pozície a orientácie korytnačky v priestore. Parametre možno použiť ako argumenty používateľom definovaných funkcií popisujúcich geometrický tvar, do akého sú stromy orezané.

3.4.8 Otvorené L-systémy (Open L-systems)

Otvorené L-systémy (Prusinkiewicz et al., 2003) rozširujú funkčnosť enviromentálnych L-systémov, a to použitím symbolov pre komunikáciu medzi rastlinou a prostredím. Prostredie sa nereprezentuje jednoduchou funkciou, ale stáva sa aktívnym procesom a môže reagovať na informácie, prichádzajúce od rastliny. Rastliny sa preto modelujú ako otvorené kybernetické systémy, ktoré odosielajú a zároveň prijímajú informáciu z prostredia (Obr. 5.11). Odovzdávanie a príjem informácie umožňujú tzv. komunikačné moduly (comunication modules).

Obr. 5.11 Simulácia interakcie rastliny s prostredím (Prusinkiewicz, 2000, Prusinkiewicz et al., 2003).

3.5 Aplikácie L-systémov

Modely rastlín založené na teórii L-systémov umožňujú (Prusinkiewicz, 2004a):

· napodobniť stavbu a rast rastlín,

· ukázať vplyv rôznych parametrov (napr. uhol vetvenia, veľkosť konárov, rýchlosť predlžovania) na výsledný vzhľad rastlín,

· simulovanie fyziologických procesov v rastline, vplyvov človeka (orezávanie, vytváranie bonsaiov) a vonkajších podmienok (vplyv svetla, vody, nedostatku miesta, prekážok) na jej vývin,

· simulovanie nielen samotných rastlín, ale celých ekosystémov.

Hoci hlavné uplatnenie L-systémov je pri modelovaní bylinných rastlín, boli použité aj na modelovanie stromov. Prusinkiewicz (1990) ukázal, že pomocou L-systémov je možné vygenerovať modely stromov, ktoré vytvorili Honda (1971) a Aono a Kunii (1984). V osobitnej práci ukázal Shebell (1986), že pomocou L-systémov sa dajú vygenerovať architektonické modely stromov, ktoré popísali Hallé, Oldeman a Tomlinson (1978). L-systémy použil pri modelovaní stromov tiež Shlyakhter (2001).

Okrem modelovania rastlín boli L-systémy použité aj na simuláciu rastu tráviacej sústavy u ľudských embryí (Ďurikovič et al., 1998), cestných sietí v mestách (CityEngine, 2007), tvorbu hudby (Prusinkiewicz, 1986b, Manousakis, 2006, LMUSe, 2007) ale aj na generovanie klasických lineárnych deterministických fraktálov (Prusinkiewicz et al., 1990, Peitgen et al., 1992).

4 Geometrická reprezentácia stromov

4.1 Reprezentácia architektúry

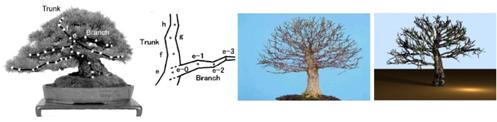
Pri modelovaní stromov, ich stavby a funkcie, si treba stanoviť spôsob reprezentácie štruktúry ich koruny, kmeňa, koreňov, teda ich architektúry. Pretože ciele modelovania sa môžu líšiť podľa aplikácií, existuje široká škála rôznych reprezentácii (Godin, 2000). Podľa neho možno stavbu rastliny reprezentovať kombináciou troch informácií:

· Dekompozícia (decomposition information) – popisuje rôzne zložky (moduly), ktoré vytvárajú rastlinu.

· Geometrická informácia (geometrical information) – popisuje tvary a priestorové umiestnenie jednotlivých zložiek. Zložky sa uvažujú nezávisle od seba.

· Topologická informácia (topological information) – popisuje vzájomný vzťah a spojenie medzi zložkami. Táto informácia vyjadruje hierarchiu medzi zložkami v systéme rozkonárenia.

Podľa stupňa komplexnosti reprezentácie rastliny, hovoríme o troch reprezentáciách:

· Globálne reprezentácie (global representations) – rastlina je reprezentovaná ako celok. V tomto prípade nie je potrebné uvažovať jednotlivé časti rastliny.

· Modulárne reprezentácie (modular representations) – spoliehajú sa na opis určitých častí rastliny (modulov), ktorých opakovaním je vytvorená celá rastlina.

· Viacúrovňové reprezentácie (multi-scale representations) – uvažujú sa hierarchie modulov majúce rôznu veľkosť.

Pre našu potrebu je zatiaľ dôležité podrobnejšie vysvetlenie modulárnej reprezentácie rastlín, ktorú popíšeme v nasledujúcej časti.

4.1.1 Modulárna štruktúra rastlín

Matematické modely v botanike zodpovedajú rôznym úrovniam organizácie rastlín (..., molekula, organela, bunka, orgán, rastlina, porast, ekosystém, bióm, ...) (Prusinkiewicz et al., 1996). Ak sa zameriame na rastlinu, môžeme ju pokladať za súbor diskrétnych stavebných jednotiek v priestore, modulov (modules), ktoré sa postupne vyvíjajú. Väčšinou moduly reprezentujú opakujúce sa základné štrukturálne časti rastliny, ako sú kvety, listy, články (internódiá), vrcholy alebo ich zoskupenia, napríklad konáre alebo články stonky s priľahlým listom alebo pazušným púčikom (Obr. 6.1). Cieľom modelovania na modulárnej úrovni je popísať vývoj rastliny ako celku a najmä vytváranie (emergence) rastlinného tvaru ako výsledku integrácie vývoja a pôsobenia jednotlivých modulov (Prusinkiewicz et al., 2003).

Obr. 6.1 Príklady modulov a ich zoskupení (upravené podľa Prusinkiewicz et al., 2003).

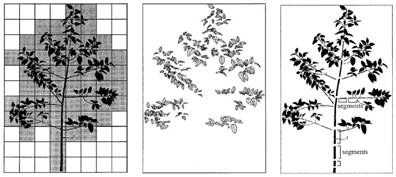
Pri modulárnej reprezentácii možno uvažovať dva základné typy dekompozície, a to priestorovú (spatial) a štrukturálnu (organ-based) dekompozíciu (Godin, 2000). Pri priestorovej dekompozícii je rozloženie modulov v priestore aproximované rozdelením priestoru na bunky konštantnej veľkosti a označením buniek, ktoré obsahujú moduly. Štrukturálna dekompozícia berie do úvahy konkrétne moduly. Môžeme ju rozdeliť na dve triedy, geometrickú a topologickú dekompozíciu. Pri geometrickej dekompozícii sa berie do úvahy len geometria modulov a ich umiestnenie v priestore, kým pri topologickej dekompozícii sa uvažujú aj spojenia medzi jednotlivými modulmi (Obr. 6.2).

Obr. 6.2 Modulárna reprezentácia rastliny, priestorová, geometrická a topologická dekompozícia (zľava doprava) (Godin, 2000).

4.2 Reprezentácia geometrie

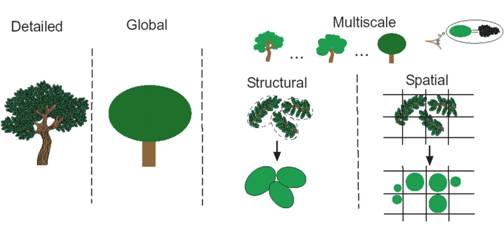
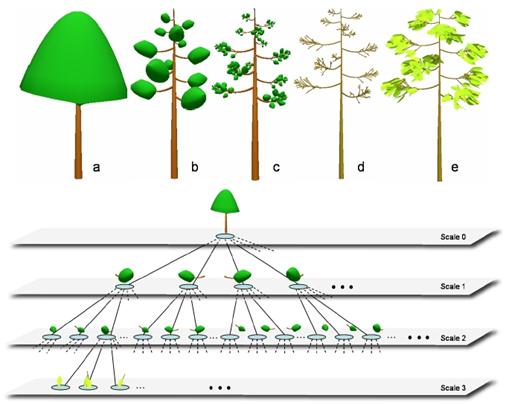
Vyššie spomínanú klasifikáciu reprezentácie rastlín ďalej rozširuje Boudon (2006), ktorý popisuje detailné, globálne a viacúrovňové reprezentácie stromov s dôrazom na realistické a efektívne zobrazenie (rendering) (Obr. 6.3). Podobne ako v predchádzajúcej časti, zameriame sa na podrobnejší popis detailnej reprezentácie rastlín.

Obr. 6.3 Reprezentácia stromov (Boudon et al., 2006).

4.2.1 Detailné reprezentácie

Detailné reprezentácie sa snažia zobraziť geometriu stromu tak, aby vyzerala realisticky aj pre blízke pohľady. Stromy majú dve odlišné časti, nerozkonárený kmeň a bohato rozkonárenú korunu (ktorú vytvárajú konáre, na ktorých spravidla rastú listy), čo si vyžaduje použitie rôznych techník na modelovanie a renderovanie jednotlivých častí stromu. V snahe dosiahnuť realistické zobrazenie, stromy sú chápané ako súbor modulov (listy, konáre a iné) a geometrický model je vytvorený ich spojením.

Konáre sú obyčajne reprezentované množinou pospájaných základných geometrických telies, na ktoré môže byť aplikovaná textúra predstavujúca kôru. Pri návrhu realistickej reprezentácie kmeňa a konárov je zložitou úlohou vytvorenie spojitého modelu z diskrétnej množiny geometrických útvarov (geometrical primitives). Preto je hlavným problémom definícia presnej reprezentácie miest, kde sa spájajú, respektíve sa vetvia konáre (branch junctions).

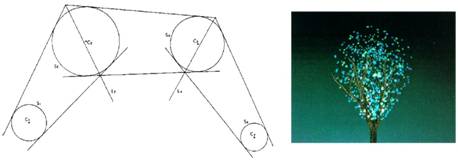
Najjednoduchšia reprezentácia konárov stromu je pomocou valcov (3D cylinders) (Obr. 6.4). Vo svojich modeloch ich používa (Kawaguchi, 1982, De Reffye et al., 1988, Prusinkiewicz et al., 1990).

Obr. 6.4 Geometria a príklad rozkonárovania s použitím mnohostenov (Kawaguchi, 1982).

Bohužiaľ, tieto techniky nezachytávajú správne geometriu tých miest, z ktorých vychádzajú nové konáre a môžu sa objaviť rôzne medzery alebo prerušenia. V snahe odstrániť tento problém bolo navrhnutých niekoľko ďalších reprezentácií.

Max (1990) predstavil novú reprezentáciu pomocou útvaru, ktorý nazýva cone-sphere. Ten pozostáva z dvoch gúľ a časti kužeľa alebo valca, ktorý leží medzi nimi a dotýka sa ich (Obr. 6.5). Vonkajší povrch spojenia je tvorený časťou gule, výsledkom čoho je plynulý prechod z jednej časti na druhú. Na vnútornej strane sa však dotyčnice pretínajú skôr, čo vedie k nespojitosti. Na zlepšenie výsledku je použitá zmiešavacia metóda (blending method) založená na jednoduchej lineárnej interpolácii. Táto reprezentácia umožňuje efektívne modelovať jednotlivé konáre, ale prináša problémy pri použití textúr v miestach spájania. V súvislosti s týmto problémom boli navrhnuté ďalšie riešenia, formulované implicitne (Hart et al., 1996, Galbraith et al., 2004).

Obr. 6.5 Cone-Sphere (Max, 1990).

Na ďalšie zlepšenie prispel Bloomenthal (1985), ktorý reprezentoval konáre pomocou zovšeobecnených valcov (generalized cylinders) (Obr. 7.2).

Bloomenthal tiež predstavil implicitné povrchy (implicit surfaces) (Bloomenthal, 1995). Na rozdiel od iných metód, implicitné povrchy umožňujú vytvoriť ľubovoľné vetviace štruktúry, bez ohľadu na ich komplexnosť. Ich výpočtová zložitosť je však vysoká (Galbraith et al., 2004a, Galbraith et al., 2004b).

Obr. 6.6 Implicitná reprezentácia topoľa (Galbraith et al., 2004a).

Alternatívnu metódu na tvorbu hladkých povrchov predstavujú subdivision surfaces (Obr. 6.7).

Obr. 6.7 Subdivision surfaces (Tobler et al., 2002).

Prehľad techník použitých na textúrovanie kôry a listov možno nájsť v (Boudon et al., 2006).

5 Modelovanie stromov

V literatúre sa stretávame s viacerými klasifikáciami, ktoré sa snažia utriediť rôzne metódy navrhnuté pre modelovanie rastlín, konkrétne stromov a zovšeobecniť výhody a nevýhody jednotlivých prístupov:

1) Rozdelenie metód na biologicky motivované (biology-based) a metódy vychádzajúce z geometrie (geometry-based) (Shlyakhter, 2001):

2) Biology-based – tieto metódy v sebe zahŕňajú biologické zákonitosti týkajúce sa rastu stromov, generujú vierohodné modely, používateľ má však len veľmi malú kontrolu nad výsledkom, hlavne výsledným tvarom stromu.

3) Geometry-based – tieto metódy ponúkajú väčšiu kontrolu výsledného tvaru, ale modely nedosahujú botanickú vernosť.

4) Quan (2006) rozširuje predchádzajúce rozdelenie na metódy založené na pravidlách (rule-based methods) alebo obrazoch (image-based methods):

5) Rule-based methods – používajú pevne stanovené pravidlá alebo gramatiky:

6) L-systémy (Prusinkiewicz et al., 1990, atď.).

7) Geometrické pravidlá (Weber et al., 1995).

8) Biologické pravidlá (De Reffye et al., 1988, atď.).

Hoci tieto metódy umožňujú vytvoriť presvedčivé modely stromov alebo celých ekosystémov, pravidlá alebo parametre, z ktorých vychádzajú sú ťažko použiteľné pre laika.

9) Image-based methods – umožňujú vymodelovať konkrétny strom na základe jeho fotografií. Použité sú rôzne prístupy:

10) Visual hull (Sakaguchi et al., 1999, Shlyakhter et al., 2001).

11) Objemová reprezentácia (Reche et al., 2004).

12) Structure from motion (Quan et al., 2006).

Nevýhodou pri týchto prístupoch je len približný tvar stromu s nerealistickou štruktúrou konárov a veľkým počtom polygónov (Shlyakhter et al., 2001) alebo prístup, ktorý neumožňuje získať explicitnú geometriu konárov a listov a výsledný model nemožno ďalej editovať (Reche et al., 2004).

13) Rozdelenie procedurálnych modelov na dve triedy – local-to-global a global-to-local modely (Prusinkiewicz et al., 2001, Boudon et al., 2003):

14) Modely local-to-global – používateľ si určí jednotlivé časti (moduly) rastliny, ktoré sa na základe použitého algoritmu spoja do komlexnej štruktúry. Kvôli emergentnému charakteru rastlín býva však ťažké kontrolovať výsledný tvar. Výnimkou sú prístupy, ktoré umožňujú kontrolovať tvar rastliny, vznikajúci ako odpoveď na orezávanie (Prusinkiewicz et al., 1994).

15) Modely global-to-local – na rozdiel od predchádzajúcich, používateľ charakterizuje celkový vzhľad rastliny ako napr. jej siluetu alebo hustotu rozloženia konárov (Reeves et al., 1985, Weber et al., 1995, Ďurikovič, 2003). Algoritmus z tejto informácie odvodí detailnejšiu štruktúru rastliny. Tento prístup ponúka priamejšiu a intuitívnejšiu kontrolu výsledného tvaru, a preto sa uprednostňuje v aplikáciách, kde je dôležitá najmä vizuálna stránka. Tieto aplikácie zahŕňajú aj odvodenie tvaru stromu z fotografií (Shlyakhter et al., 2001, Quan et al., 2006) a interaktívnu kontrolu tvaru (Prusinkiewicz et al., 2001, Boudon et al., 2003, Lintermann et al., 1999, Deussen et al., 2005). Výhodou týchto prístupov je, že parametre použité pre tvorbu detailnejšej stavby sú odvodené (zdedené) z parametrov popisujúcich celkovú stavbu stromu. Nevýhodou pri interaktívnom modelovaní je to, že ide o zdĺhavý proces a ľahko sa môže stať, že používateľ sa zamotá, ak si stanoví veľký počet parametrov a stráca tak možnosť intuitívnej kontroly nad modelom. Tento problém sa však dá vyriešiť použitím viacúrovňovej reprezentácie rastlín (multiresolution editing) (Boudon et al., 2003).

Simulácia vetviacich štruktúr má v počítačovej grafike relatívne dlhú históriu. Prvý model, ktorý bol navrhnutý, vychádza z koncepcie celulárnych automatov (cellular automata) (Ulam, 1966). Vetviaci vzor (branching pattern) sa vytvára iteratívne, začínajúc jedinou farebnou bunkou v trojuholníkovej mriežke. Postupne sa farbia bunky, ktoré sa dotýkajú práve jedného vrchola bunky, ktorá bola zafarbená v predchádzajúcom iteračnom kroku.

Pre tento prístup (a jeho ďalšie rozšírenia) je charakteristický dôraz na interakciu medzi rôznymi časťami rastúcej štruktúry a rovnako štruktúry a prostredia. Hoci interakcie ovplyvňujú vývoj rastlín, pridávajú tiež na zložitosti modelov. To vysvetľuje, prečo jednoduché modely, ktoré ignorujú aj základné faktory, napríklad kolíziu medzi konármi, prevládajú dodnes.

Obr. 7.1 Špecifikácia geometrie stromu podľa Hondu (1971).

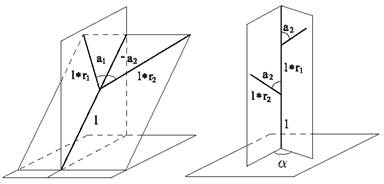
Prvý jednoduchý model stromu navrhol Honda (1971), ktorý študoval tvary stromov s použitím nasledujúcich pravidiel (Obr. 7.1):

· Segmenty stromu sú rovné, ich hrúbka (obvod) sa neuvažuje.

· Materský segment vytvorí počas jedného rozkonárovania (branching process) dva dcérske segmenty.

· Dĺžky dcérskych segmentov sa skrátia konštantnými škálovacími koeficientmi a , vzhľadom na materský segment.

· Materský segment a jeho dva dcérske segmenty ležia v jednej rovine (branch plane). Dcérske segmenty vytvárajú vzhľadom na materský segment konštantné uhly (branching angles) a .

· Rovina rozkonárenia je vzhľadom na gravitáciu pevne stanovená, a to tak, aby bola čo najbližšie k horizontálnej rovine. Výnimku tvoria vetvy, ktoré vyrastajú z hlavného kmeňa. V ich prípade sa zachová konštantný uhol odchýlky (divergence angle) medzi za sebou vychádzajúcimi bočnými segmentmi.

Zmenou parametrov získal širokú škálu tvarov, podobajúcich sa na stromy a vďaka ďalším vylepšeniam sa jeho model používal na skúmanie spôsobov rozkonárovania u reálnych stromov.

Niekoľko ďalších rozšírení založených na jeho výsledkoch navrhli Aono a Kunii (1984). Zároveň boli prvými autormi, ktorý skúmali použitie L-systémov na tvorbu botanických stromov. Vychádzali z pôvodnej definície L-systémov, pričom zistili, že je nevhodná na modelovanie rozkonárených štruktúr u vyšších rastlín.

Doteraz spomínané modely reprezentovali „kostru stromu“ s použitím rovných čiar konštantnej alebo meniacej sa hrúbky. Podstatné realistické vylepšenie modelov dosiahli Bloomenthal (1985) a Oppenheimer (1986), ktorí predstavili oblé konáre, dôkladne namodelované povrchy v miestach rozkonárenia a otextúrovanú kôru a listy.

Bloomenthal sa namiesto štúdia rôznych typov rozkonárovania zameral na zlepšenie realizmu výsledného modelu (Obr. 7.2). Stromy reprezentoval ako množinu bodov v priestore a ich spojení (konárov). Konáre sú modelované ako "zovšeobecnené valce" (generalized cylinders), ktoré sú reprezentované ako priestorové krivky interpolujúce body a postupnosť obrysov (cross sectional contour) kolmých na krivku. Povrch stromu sa teda znázorňuje ako zovšeobecnený valec s pospájanými kruhovitými (konáre) alebo zakrivenými (kmeň) obrysmi rôzneho polomeru.

Obr. 7.2 Špecifikácia geometrie stromu podľa Bloomenthala (Bloomenthal, 1985).

Oppenheimer zaviedol fraktálny model stromu, ktorého geometria a topológia je kontrolovaná číselnými parametrami analogickými ku DNA živých organizmov. Zmenou genetickej informácie (parametrov) nastáva zmena geometrie objektu, výsledný model však ostáva samopodobný, hoci menením parametrov to nemusí byť až také viditeľné (Obr. 7.3).

Obr. 7.3 Fraktálny model stromu a stonky a listov maliny (Oppenheimer, 1986).

Reeves a Blau (1985) sa zamerali na tvorbu lesných scén a použitím stochastického prístupu, systému častíc (particle systems), vytvárali veľmi komplexné obrázky, ktoré ale nerešpektovali biologické zákonitosti (Obr. 7.4).

Obr. 7.4 Lesná scéna vytvorená pomocou systému častíc (Reeves et al., 1985).

De Reffye (1988) navrhol model stromu, ktorý vychádza z biologických zákonitostí (ako stromy rastú, obsadzujú priestor, kde a ako vyrastajú listy, kvety alebo plody). Nezameriava sa na geometriu stromu ako Bloomenthal, ale zdôrazňuje skôr topologický model stromu. Hlavná myšlienka spočíva v modelovaní aktivity púčikov v diskrétnych časových intervaloch. Na základe signálu môže púčik:

· stať sa kvetom a odumrieť (a zaniknúť),

· zmeniť sa na spiaci púčik,

· predĺžiť sa na článok (internódium), ktorý bude ukončený novým vrcholovým púčikom a jedným alebo viacerými bočnými púčikmi, ktoré sa objavia v pazuchách listov.

Tieto zmeny sa dejú na základe stochastických zákonov charakteristických pre jednotlivé druhy a variety. Podľa stochastických pravidiel sú tiež vypočítané geometrické parametre, ako napríklad dĺžka a priemer článkov alebo uhol vetvenia. Všetky pravdepodobnostné zákonitosti môžu byť merané experimentálne, napríklad na poľnohospodárske ciele, a merania môžu potvrdiť správnosť modelu. Zmenou pravdepodobností možno získať architektonické modely drevín, ktoré popísali Hallé, Oldeman a Tomlinson (1978).

Sila takéhoto prístupu spočíva v tom, že pomocou tých istých procedurálnych metód možno vytvoriť rôzne modely rastlín, od drevín ako napríklad jedľa, borovica, čerešňa, vŕba, topole až po bylinné druhy (Obr. 7.5).

Obr. 7.5 Ukážky modelov stromov vytvorených podľa (De Reffye et al., 1988).

Obr. 7.6 Ukážky modelov stromov vytvorených podľa Webera (1995).

Weber a Penn (1995) sa namiesto rešpektovania biologických zákonitostí pri modelovaní stromov zamerali na celkový geometrický tvar. Ich model je založený na dvoch častiach, stonke (kmeň a konáre) a liste. Kmeň stromu pozostáva zo zaoblených kužeľovitých častí, ktoré sa môžu na rôznych miestach rozdeliť a vytvoriť nové valcovité štruktúry, ktoré sa môžu ďalej deliť (rozkonárovať). Mnohé atribúty nových konárov (napr. dĺžka) sú odvodené od rodičovských, môžu však byť aj úplne iné. Použitím malého počtu parametrov vytvorili len na základe pozorovania a porovnávania tvarov reálnych stromov, niekoľko rôznych modelov stromov podobných reálnym druhom (Obr. 7.6). Autori tiež predstavili viacúrovňovú reprezentáciu stromov, umožňujúcu efektívne zobrazovanie väčšieho počtu stromov v scéne.

Viacerí autori publikovali rôzne procedurálne metódy umožňujúce generovať stromy, Sakaguchi (Sakaguchi et al., 1999) sa však zameral na inverzný problém, a to ako odvodiť tieto metódy pre konkrétny strom, na základe jeho fotografií. Takáto potreba môže vzniknúť ak chceme vytvoriť model nejakého konkrétneho stromu (napr. historicky alebo kultúrne významného), nachádzajúceho sa v scéne. Hľadať parametre, z ktorých by sme mohli odvodiť tvar daného stromu je príliš zdĺhavé a intuitívne a môže spôsobiť veľa neželaných efektov.

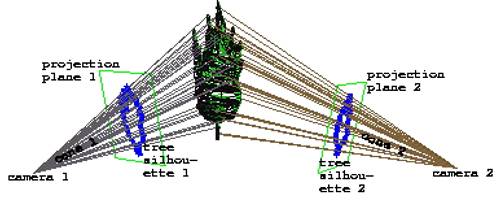
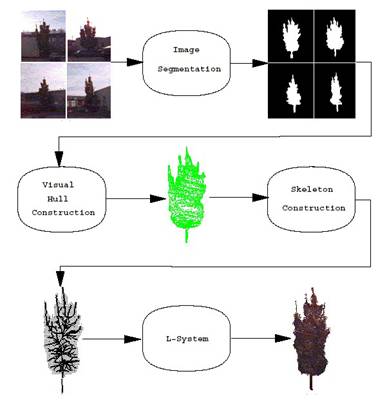
Tento prístup vylepšil Shlyakhter (Shlyakhter et al., 2001), ktorý odvodzuje hlavnú štruktúru (kostru) stromu priamo z jeho celkového tvaru. Vychádza z fotografií stromu, štyroch až pätnástich, ktoré zachytávajú najmenej 135° okolo stromu. Pozícia a orientácia fotoaparátu pre každý obrázok je známa. Proces rekonštrukcie pozostáva zo štyroch krokov (Obr. 7.8):

1) Segmentácia obrázkov − všetky obrázky sú segmentované na strom a pozadie. Tento proces je manuálny, v grafickom editore sa naznačí obrys, silueta stromu.

2) Visual hull − každá silueta získaná zo vstupných fotografií sa aproximuje mnohouholníkom. Projekciou jeho obrysu vzniká „kužeľ“ (n-boký nekonvexný ihlan), ktorý ohraničuje 3D strom ležiaci v ňom, takže vypočítaním prieniku všetkých kužeľov, vznikne aproximácia trojrozmerného tvaru stromu, visual hull (Laurentini, 1994).

Obr. 7.7 Rekonštrukcia tvaru stromu zo siluet (Shlyakhter et al., 2001).

3) Vytvorenie kostry stromu − kostra stromu (kmeň a niekoľko ďalších stupňov rozkonárenia) je hľadaná ako aproximácia osi (medial axis) obalu (visual hull). Autori vychádzajú z myšlienky, že stromy sa v snahe prijať čo najviac slnečnej energie potrebnej pre fotosyntézu, snažia rozložiť konáre v priestore čo najefektívnejšie. Tieto pozorovania naznačujú, že kostru stromu možno prirovnať ku osi jeho tvaru, ktorá predstavuje v istom zmysle optimálnu kostru.

4) L-systém − vytvorená kostra stromu sa použije ako axióma pre otvorený L-systém, ktorý pridá posledným dvom stupňom konárov púčiky, ktoré umožnia rast ďaších konárov a listov. L-systém zároveň zabezpečí rozloženie konárov a listov a tiež to, aby všetky konáre, ktoré prerastú tvar stromu, boli odrezané.

Obr. 7.8 Proces rekonštrukcie 3D modelu stromu z fotografií (Shlyakhter et al., 2001).

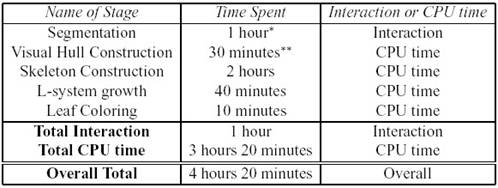
Obr. 7.9 Časová náročnosť jednotlivých krokov rekonštrukcie (Shlyakhter et al., 2001).

Veľkou nevýhodou tejto metódy je okrem značnej prácnosti a vysokého počtu polygónov, len približná kostra stromu, ktorá nie je obrazom reálneho rozkonárenia (Obr. 7.10).

Obr. 7.10 Ukážky kostry stromu a porovnanie fotografie reálneho stromu s vytvoreným modelom (zľava doprava) (Shlyakhter et al., 2001).

Poloautomatickú, interaktívnu techniku na modelovanie rastlín priamo z fotografií navrhol Quan (2006). Výsledný model je geometrický a môžno s ním ľahko manipulovať, prípadne ho ďalej editovať.

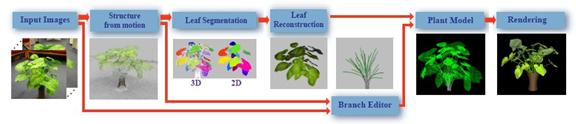
Obr. 7.11 Proces rekonštrukcie modelu z fotografií (Quan et al., 2006).

Ich metóda pozostáva z troch krokov (Obr. 7.11):

1) Získanie obrazov (fotografií) a použitie algoritmu structure from motion – vstupné dáta predstavuje 30 až 45 vzájomne sa prekrývajúcich fotografií, voľne vzatých dookola rastliny, tak aby bola rastlina zachytená z viacerých pohľadov. Fotoaparát nemusí byť kalibrovaný, malo by sa však vyhnúť zmenám expozície v dôsledku nerovnakého osvetlenia alebo tieňov. Ďalej sa použije structure from motion algoritmus (Lhuiller et al., 2005), vďaka ktorému sa získajú parametre fotoaparátu a oblak 3D bodov. Tieto body pomôžu pri určení tvaru rastliny. Každý bod je spojený s informáciou o tom, z ktorej fotografie pochádza, čo má význam pri ďalších krokoch, a to segmentácii listov a konárov.

2) Segmentácia a rekonštrukcia listov – pomocou navrhnutej graph-based optimalizačnej techniky sa 3D body a pixely fotografií súčasne rozdelia do diskrétnych množín, kde každá množina reprezentuje jeden list. Táto časť procesu segmentácie prebieha automaticky, ale v ďalšom kroku môže do nej vstúpiť aj používateľ, ktorý môže interaktívnym spôsobom zefektívniť a vylepšiť proces segmentácie. Po každej zmene sa systém hneď aktualizuje. Keďže listy rastliny sú prevažne rovnaké, na rekonštrukciu listov si používateľ vyberie jeden vzorový list, ktorý je ďalej upravený a použitý namiesto ostatných listov, čo zvyšuje robustnosť systému (Obr. 7.12).

3) Interaktívna rekonštrukcia konárov – kým listy sú rekonštruované prevažne automaticky, pri konároch je to kvôli ich komplexnosti problém. Autori považujú rekonštrukciu konárov pomocou L-systémov za zložitú, pretože používateľ nemusí vedieť, aké vstupné parametre použiť, aby dostal výsledný tvar. Namiesto použitia L-systémov, navrhli editor, ktorý umožňuje interaktívnym spôsobom kontrolovať výsledný tvar konárov. Konáre sú modelované ako zovšeobecnené valce (generalized cylinders), ktorých os tvorí priestorová krivka. Samotný proces rekonštrukcie pozostáva z niekoľkých krokov. Používateľ najskôr kreslí krivky, ktoré reprezentujú jednotlivé konáre a následne ich na základe vstupných fotografií pre ľubovoľné pohľady upravuje, mení ich umiestenie v priestore, tvar, polomer alebo určuje, či na konci konára budú rásť listy (Obr. 7.12). Výsledný model vznikne spojením rekonštruovaných konárov a listov, ktoré sú automaticky pripojené k najbližším konárom.

Obr. 7.12 Segmentácia a rekonštrukcia listov a konárov (zľava doprava) (Quan et al., 2006).

Metóda bola testovaná na izbových rastlinách, kde ponúkala veľmi dobré výsledky, vďaka malému počtu konárov a veľkým listom. Bola vyskúšaná aj na modelovanie menšieho (izbového) stromu, v tomto prípade sa však kvôli väčšej komplexnosti objektu (väčší počet konárov aj listov, ktoré sú navyše menšie, v porovnaní s izbovými rastlinami) zvýšila výpočtová zložitosť a výsledok bol menej presný (Obr. 7.13).

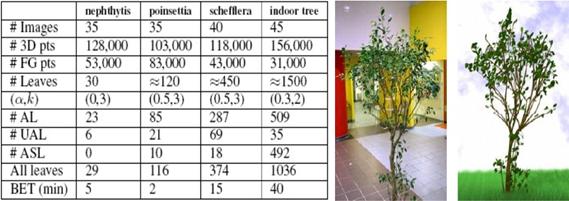
Obr. 7.13 Štatistika rekonštrukcie a porovnanie fotografie stromu s modelom. FG – foregrounds, AL – automatic leaves, UAL – user assisted leaves, ASL – additional synthetic leaves, BET – branch edit time (Quan et al., 2006).

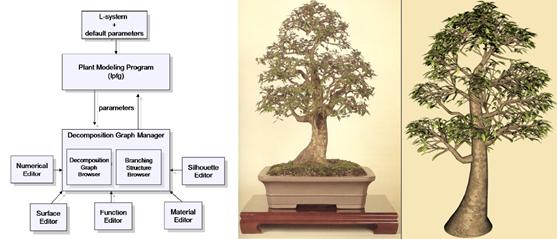
Ďurikovič (2003) predstavil metódu na modelovanie presného tvaru stromov, ktorú ukázal na modelovaní bonsaiov, u ktorých je podstatný práve ich vonkajší tvar. Tvar je odvodený z fotografií stromu a nameraných dát. Na základe nameraných dát pre vybrané konáre odvodí funkciu aproximujúcu dáta, ktoré sú použité na vytvorenie L-systému, schopného reagovať na vonkajšie vplyvy prostredia, prijímať a zároveň odovzdávať informácie pomocou komunikačných modulov. L-systém vygeneruje kostru stromu (hlavné konáre vytvárajúce tvar stromu), majúcu rovnaký tvar ako odvodená funkcia. Pomocou L-systému sú generované aj drobné konáre (konáre vyššieho stupňa) a listy. Tie sú rozmiestnené okolo hlavných konárov podľa funkcie určujúcej hustotu rozloženia. Konáre sú reprezentované ako zrezané kužele vychádzajúce z uzlov, s výškou odvodenou od ich začiatočného a koncového polomeru. Polomer zodpovedá aktuálnej hrúbke konáru danej jeho umiestnením. Kým parametre hlavných konárov sú dané z nameraných dát, parametre menších konárov sú vypočítané náhodne z priemerných hodnôt. Listy sú reprezentované ako trojuholníková sieť a ihlice ako dlhé úzke kužele.

Obr. 7.14 Znázornenie meraných bodov a porovnanie fotografie s vygenerovaným stromom (Ďurikovič, 2003).

Metódu na kontrolovanie veľkého množstva vstupných parametrov potrebných pri detailnejšom popise a modelovaní rastlín navrhol (Boudon et al., 2003) a ilustroval ju na interaktívnom modelovaní bonsaiov. Ide o viacúrovňovú reprezentáciu, pri ktorej popisujú štruktúru rastlín pomocou decomposition graph. Je to strom (v teoretickom zmysle), ktorý zachytáva hierarchickú štruktúru rastliny, na základe stupňa rozkonárenia (Obr. 7.15). Uzly tohto grafu obsahujú parametre, ktoré popisujú časti stromu na jednotlivých hierarchických úrovniach, a teda na rôznych stupňoch detailu. V procese interaktívneho modelovania stromu sú parametre popisujúce vyššie stupne konárov zdedené z parametrov popisujúcich strom ako celok. Používateľ môže manipulovať s týmito parametrami alebo ich editovať bez ohľadu na dedičnosť. Model je vytváraný algoritmicky, s parametrami uloženými v decomposition graph. Na začiatku modelovacieho procesu si používateľ špecifikuje algoritmus (L-systém), ktorý vytvorí decomposition graph a definuje parametre pre niektoré uzly. Pre tie uzly, ktoré nemali explicitne definované parametre, sú parametre zdedené. Následne môžu byť parametre interaktívne editované. Pri každej zmene sa algoritmus znovu spustí a výsledný tvar stromu sa aktualizuje (Obr. 7.16).

Obr. 7.15 Viacúrovňová reprezentácia štruktúry stromu (hore) a príslušný decomposition graph (dole) (Boudon et al., 2003).

Obr. 7.16 Interakcia rôznych komponentov počas procesu modelovania (vľavo), porovnanie fotografie s modelom (vpravo) (Boudon et al., 2003).

6 Aplikácie virtuálnych modelov rastlín

Modelovanie rastlín má medzivedný charakter a odráža diverzitu existujúcich a možných aplikácií modelov (Prusinkiewicz, 2004a).

· Vedecké využitie:

· Biológia – výskum hypotéz týkajúcich sa genetických, fyziologických alebo biomechanických zákonitostí rastu rastlín alebo biologických štruktúr. Klasifikácia architektúry (vonkajšej stavby, tvaru) rastlín.

· Ekológia – skúmanie vzťahov medzi samotnými rastlinami a tiež rastlinami a prostredím.

· Evolúcia – analýza tvaru rastlín z pohľadu evolúcie.

· Praktické využitie, kde je podstatná architektúra rastlín:

· Šľachtenie rastlín a genetické inžinierstvo – špecifikácia "cieľovej" rastliny na základe určenia stavby tela optimálnej pre príjem slnečného žiarenia, úrodnosť, odolnosť voči poškodeniu, kvalitu a kvantitu plodov, kvetov, vzhľadu, atď.

· Ošetrovanie rastlín – určenie stratégii rastlín pri obsadzovaní priestoru a optimálne ošetrovanie (orezávanie, použitie chemikálií, stanovenie vhodnej teploty) v ovocných sadoch, skleníkoch, záhradách alebo v bytoch.

· Krajinná architektúra – simulácia interakcií medzi stromami a rôznymi stavbami, napr. spôsob odstraňovania konárov, aby sa zabránilo kolízii s elektrickým vedením.

· Praktické využitie, kde nie je podstatná architektúra rastlín, ale jej zahrnutie môže vylepšiť hodnotu predpovedných modelov:

· Simulovanie prítomnosti a šírenia patogénov u rastlín.

· Biologická kontrola prítomnosti burín (inváznych druhov) – skúmanie ich stavby a vplyvu rôznych patogénov alebo prítomnosti bylinožravcov na ich výskyt.

· Simulovanie vplyvu pesticídov.

· Aplikácie vo vyučovaní:

· Vysvetlenie a ilustrácia procesov prebiehajúcich v rastlinách, vzťahov medzi rastlinou a prostredím. Využitie vo vyučovacom procese, pri cvičeniach.

Virtuálne modely rastlín prispievajú k pochopeniu rôznych mechanizmov prebiehajúcich v rastlinách počas ich rastu. Napriek tomu je ich využitie v praxi (napr. v záhradníctve, poľnohospodárstve, lesníctve) zatiaľ nevýrazné. Prusinkiewicz (2004a) naznačuje niekoľko faktorov, ktoré môžu byť príčinou tohto stavu:

· Fyziologické mechanizmy ovplyvňujúce funkciu rastlín nie sú natoľko známe, aby mohli poskytnúť pevný základ pre tvorbu prognostických modelov. Ešte menej je známe o genetickej podstate vývinu rastlinných foriem.

· Metódy na modelovanie rastlín a tvorba príslušného softvéru patria stále do oblasti aktívneho výskumu a bude chvíľu trvať kým sa začnú používať na riešenie praktických problémov.

· Tvorba rastlinných modelov je úsilím viacerých vedných odborov. Kombinuje v sebe rôzne aspekty biológie, matematiky, počítačovej grafiky a špecifických modelovacích zručností (umenia), preto je ťažké nájsť ľudí alebo vytvoriť tímy, ktoré by mali žiadané odborné znalosti.

· Tvorba presných modelov vyžaduje rozsiahle merania rastlín, a preto je drahá.

Otvoreným problémom tiež zostáva začlenenie genetických mechanizmov do virtuálnych rastlín, čo by mohlo priniesť nový pohľad na pochopenie vývinových procesov u rastlín.

V práci sme predstavili prehľad metód na modelovanie stromov. Existuje viacero programov, ktoré umožňujú viac či menej realistické modelovanie stromov. Medzi najznámejšie patrí XFrog, SpeedTree, vlab/L-studio. Prehľad jednotlivých programov spolu s požiadavkami na systém, výhodami a nevýhodami možno nájsť na stránke Virtual Terrain Project (Plant Generation Software Packages, 2007).

Zoznam bibliografických odkazov

ABELSON, H., DISESSA, A.A. 1982. Turtle geometry. Cambridge : M:I:T: Press, 1982. Zroj: PRUSINKIEWICZ, P., LINDENMAYER, A. The algorithmic beauty of plants. New York : Springer Verlag, 1990

Adobe Photoshop [online] [cit. 2007-04-12]. Dostupné na internete: <http://www.adobe.com/products/photoshop/photoshop/>.

AKENINE-MÖLLER, T., HAINES, E., 2002. Real-time rendering. 2nd ed. AK Peters, 2002.

AONO, M., KUNII, T.L. 1984. Botanical tree image generation. IEEE Computer Graphics and Applications. 1984, vol. 4, no. 5, p. 10-34. Zroj: PRUSINKIEWICZ, P., LINDENMAYER, A. The algorithmic beauty of plants. New York : Springer Verlag, 1990

BLOOMENTHAL, J. 1985. Modeling the mighty maple. In SIGGRAPH ’85: Proceedings of the 12th annual conference on Computer graphics and interactive techniques, 1985, p. 305-311.

BLOOMENTHAL, J. 1995. Skeletal design of natural forms. PhD thesis. University of Calgary, 1995. Zdroj: BOUDON, F., MEYER, A., GODIN, Ch. 2006. A survey of computer representations of trees for realistic and efficient rendering. Report de recherche. In LIRIS, 2006.

BOBÁK, M. et al. 1992. Botanika : Anatómia a morfológia rastlín. Bratislava : SPN, 1992.

BOUDON, F., PRUSINKIEWICZ, P., FEDERL, P. et al. 2003. Interactive design of bonsai trees. In Computer Graphics Forum. Proceedings of Eurographics, 2003, vol. 22, no. 3, p. 591-599.

BOUDON, F., MEYER, A., GODIN, Ch. 2006. A survey of computer representations of trees for realistic and efficient rendering. Report de recherche. In LIRIS, 2006.

CityEngine [online] [cit. 2007-04-12]. Dostupné na internete: <http://www.vision.ee.ethz.ch/~pmueller/wiki/CityEngine/Documents>.

COOMBES, A.J. 2001. Stromy. 2. vyd. Martin : Osveta, 2001. ISBN 80-8063-066-6.

DE REFFYE, P., EDELIN, C., FRANÇON, J. 1988. Plant models faithful to botanical structure and development. In SIGGRAPH ’88: Proceedings of the 15th annual conference on Computer graphics and interactive techniques, 1988, p. 151-158.

DEUSSEN, O., LINTERMANN, B. 1997. A modelling method and user interface for creating plants. In Proceedings of the conference on Graphics Interface ’97, 1997, p. 189-197.

DEUSSEN, O., LINTERMANN, B. 2005. Digital Design of Nature : Computer Generated Plants and Organics. Berlin : Springer-Verlag, 2005. ISBN 3-540-40591-7.

ĎURIKOVIČ, R., KANEDA, K., YAMASHITA, H. 1998. Animation of biological organ growth based on L-systems. In Computer Graphics Forum, 1998, vol. 17, no. 3, p. 1-13.

ĎURIKOVIČ, R. 2003. Towards visual modelling of bonsai trees. In Proceedings of the IASTED Visualization, Imaging, Image Processing – VIIP2003, 2003, p. 797-802.

EBERT, D.S., MUSGRAVE, F.K., PEACHEY, D. et al. 1998. Texturing and modeling : A procedural approach. 2nd ed. USA : Academic Press, 1998.

Environmental Information Laboratory [online] [cit. 2007-04-12]. Dostupné na internete: <http://www.h.chiba-u.jp/terra/envinf4.htm>.

FABRIKA, M., Ďurský, J. 2005. Stromové rastové simulátory. Zvolen : EFRA – Vedecká agentúra pre ekológiu a lesníctvo, 2005. ISBN 80-969434-7-2.

FERRARO, P., GODIN, Ch., PRUSINKIEWICZ, P. 2005. Toward a quantification of self-similarity in plants. In Fractals, 2005, vol. 13, no. 2, p. 91-109.

GALBRAITH, C., MACMURCHY, P., WYVILL, B. 2004a. BlobTree Trees. In CGI ’04: Proceedings of the Computer Graphics Interactional (CGI ’04), 2004, p. 78-85.

GALBRAITH, C., MÜNDERMANN, L., WYVILL, B. 2004b. Implicit visualization and inverse modeling of growing trees. In Computer Graphics Forum (Proceedings of Eurographics 2004), 2004, vol. 23, no. 3, p. 351-360.

GODIN, Ch. 2000. Representing and encoding plant architecture: a review. In Annals of Forest Science, 2000, vol. 57, no. 05-juin, p. 413-438.

Growth model SIBYLA [online] [cit. 2007-04-12]. Dostupné na internete: <http://www.uni-forst.gwdg.de/~mfabrik/>.

HALLÉ, F., OLDEMAN, R.A.A., TOMLINSON, P.B. 1978. Tropical trees and forests: An architectural analysis. Berlin : Springer Verlag, 1978. Zroj: PRUSINKIEWICZ, P., LINDENMAYER, A. The algorithmic beauty of plants. New York : Springer Verlag, 1990.

HART, J.C., BAKER, B. 1996. Implicit modeling of tree surfaces. In Implicit surfaces ’96, 1996, p. 143-152.

HIEKE, K. 1978. Praktická dendrologie (1, 2). Praha : SZN, 1978.

HONDA, H. 1971. Description of the form of trees by the parameters of the tree-like body: Effects of the branching angle and the branch length on the shape of the tree-like body. In Journal of Theoretical Biology, 1971, 31, p. 331-338. Zroj: PRUSINKIEWICZ, P., LINDENMAYER, A. The algorithmic beauty of plants. New York : Springer Verlag, 1990.

KAWAGUCHI, Y. 1982. A morphological study of the form of nature. In SIGGRAPH ’82: Proceedings of the 9th annual conference on Computer graphics and interactive techniques, 1982, p. 223-232.

KURTH, W. 1994. Growth Grammar Interpreter GROGRA 2.4 : A software tool for the 3-dimensional interpretation of stochastic, sensitive growth grammars in the context of plant modelling. Introduction and Reference Manual. Forschungszentrum Waldökosysteme der Universität Göttingen, Göttingen, 1994.

LAURENTINI, A. 1994. The visual hull concept for silhouette-based image understanding. In IEEE Trans. Pattern Anal. Mach. Intell, 1994, vol. 16, no. 2, p. 150-162.

LHUILLIER, M., QUAN, L. 2005. A quasi-dense approach to surface reconstruction from uncalibrated images. In IEEE Trans. Pattern Anal. Mach. Intell., 2005, vol. 27, no. 3, p. 418-433.

LINTERMANN, B., DEUSSEN, O. 1999. Interactive modeling of plants. In IEEE Comput. Graph. Appl., 1999, vol. 19, no. 1, p. 56-65.

LMUSe [online] [cit. 2007-04-12]. Dostupné na internete: <http://www.geocities.com/Athens/Academy/8764/lmuse/lmuse.html>.

MALÁ, B., MLADÝ, L., MALÝ, M. 2000. Generálna rekonštrukcia areálu zámku Budatín. Žilina : MGM, 2000.

MANDELBROT, B.B. 1982. The fractal geometry of nature. San Francisco : W. H. Freeman, 1982. Zdroj: PRUSINKIEWICZ, P., LINDENMAYER, A. The algorithmic beauty of plants. New York : Springer Verlag, 1990.

Mandelbrot set [online] [cit. 2007-04-12]. Dostupné na internete: <http://en.wikipedia.org/wiki/Mandelbrot_set>.

MANOUSAKIS, S. 2006. Musical L-systems. Master’s thesis. The Royal Conservatory, The Hague, 2006.

MAX, N. 1990. Cone-spheres. In SIGGRAPH ’90: Proceedings of the 17th annual conference on Computer graphics and interactive techniques, 1990, p. 59-62.

MĔCH, R., PRUSINKIEWICZ, P., HANAN, J. [online]. Extensions to the graphical interpretation of L-systems based on turtle geometry [cit. 2007-04-12]. Dostupné na internete: <http://algorithmicbotany.org/lstudio/graph.pdf>.

NAKAMURA, A., LINDENMAYER, A., AIZAWA, K. 1986. Some systems for map generation. In ROZENBERG, G., SALOMAA, A. (eds.) The Book of L. Berlin : Springer-Verlag, 1997, p. 323-332. Zdroj: PRUSINKIEWICZ, P., LINDENMAYER, A. The algorithmic beauty of plants. New York : Springer Verlag, 1990.

OPPENHEIMER, P.E. 1986. Real time design and animation of fractal plants and trees. In SIGGRAPH Comput. Graph., 1986, vol. 20, no. 4, p. 55-64.

PEITGEN, H.-O., JÜRGEN, H., SAUPE, D. 1992. Chaos and fractals : New frontiers of science. New York : Springer Verlag, 1992. ISBN 0-387-97903-4.

Plant Generation Software Packages [online]. [cit. 2007-04-12]. Dostupné na internete: <http://www.vterrain.org/Plants/plantsw.html>.

PRUSINKIEWICZ, P. 1986a. Graphical applications of L-systems. In Proceedings on Graphics Interface ’86 / Vision Interface ’86, 1986, p. 247-253.

PRUSINKIEWICZ, P. 1986b. Score generation with L-systems. In Proceedings of the 1986 International Computer Music Conference, p. 455-457.

PRUSINKIEWICZ, P., LINDENMAYER, A. 1990. The algorithmic beauty of plants. New York : Springer Verlag, 1990.

PRUSINKIEWICZ, P., JAMES, M., MĔCH, R. 1994. Synthetic topiary. In SIGGRAPH ’94: Proceedings of the 21th annual conference on Computer graphics and interactive techniques, 1994, p. 351-358.

PRUSINKIEWICZ, P., HAMMEL, M., MĔCH, R. et al. 1995. The artificial life of plants. In Artificial life for graphics, animation, and virtual reality, SIGGRAPH ’95 Course Notes [online], 1995, vol. 7, p. 1-1-1-38. [cit. 2007-04-12]. Dostupné na internete: <http://algorithmicbotany.org/papers/l-sys.sig95.pdf>.

PRUSINKIEWICZ, P., HAMMEL, M.. 1997. Visual models of plant development. In ROZENBERG, G., SALOMAA, A. (eds.) Handbook of formal languages, vol. 3: beyond words. Springer-Verlag, 1997.

PRUSINKIEWICZ, P. 2000. Simulation modeling of plants and plant ecosystems. In Commun. ACM, 2000, vol. 43, no. 7, p. 84-93.

PRUSINKIEWICZ, P., MUENDERMANN, L., KARWOWSKI, R. et al. 2001. The use of positional information in the modeling of plants. In SIGGRAPH ’01: Proceedings of the 28th annual conference on Computer graphics and interactive techniques, 2001, p. 289-300.

PRUSINKIEWICZ, P. et al. 2003. L-systems and beyond. In SIGGRAPH 2003 Course Notes [online]. [cit. 2007-04-12]. Dostupné na internete: <http://algorithmicbotany.org/papers/sigcourse.2003.pdf>.

PRUSINKIEWICZ, P. 2004a. Art and science for life: Designing and growing virtual plants with L-systems. In DAVIDSON, C., FERNANDEZ, T. (eds.) Nursery Crops: Development, Evaluation, Production and Use: Proceedings of the XXVI International Horticultural Congress. Acta Horticulturae, 2004, no. 630, p. 15-28.

PRUSINKIEWICZ, P. 2004b. Self-similarity in plants: Integrating mathematical and biological perspectives. In NOVAK, M. (ed.) Thinking in Patterns. Fractals and Related Phenomena in Nature. Singapore : World Scientific, 2004, p. 103-118.

QUAN, L., TAN, P., ZENG, G. et al. 2006. Image-based plant modeling. In ACM Trans. Graph., 2006, vol. 25, no. 3, p. 599-604.

REEVES, W.T., BLAU, R. 1985. Approximate and probabilistic algorithms for shading and rendering structured particle systems. In SIGGRAPH ’85: Proceedings of the 12th annual conference on Computer graphics and interactive techniques, 1985, p. 313-322.

RECHE-MARTINEZ, A., MARTIN, I., DRETTAKIS, G. 2004. Volumetric reconstruction and interactive rendering of trees from photographs. In ACM Trans. Graph., 2004, vol. 23, no. 3, p. 720-727.

Remphrey [online] [cit. 2007-04-12]. Dostupné na internete: <http://home.cc.umanitoba.ca/~remphre/research.shtml>.

RUZON, M., TOMASI, C. 2000. Alpha estimation in natural images. In Proceedings IEEE Conference and Computer Vision and Pattern Recognition, 2000, p. 597-604.

SAKAGUCHI, T., OHYA, J. 1999. Modeling and animation of botanical trees for interactive virtual enviroments. In VRST '99: Proceedings of the ACM symposium on Virtual reality software and technology, 1999, p. 139-146.

SHEBELL, M. 1986. Modeling branching plants using attribute L-systems. Master’s thesis. Worcester Polytecnic Institute, 1986. Zroj: PRUSINKIEWICZ, P., LINDENMAYER, A. The algorithmic beauty of plants. New York : Springer Verlag, 1990.

SHLYAKHTER, I., ROZENOER, M., DORSEY, J. et al. 2001. Reconstructing 3D tree models from instrumented photographs. IEEE Comput. Graph. Appl., 2001, vol. 21, no. 3, p. 53-61.

SMITH, A.R. 1984. Plants, fractals and formal languages. In SIGGRAPH ’84: Proceedings of the 11th annual conference on Computer graphics and interactive techniques, 1984, p. 1-10.

Species XML File Format [online] [cit. 2007-04-12]. Dostupné na internete: <http://www.vterrain.org/Implementation/Formats/species.html>.

TOBLER, R.F., MAIERHOFER, S., WILKIE, A. 2002. Mesh-based parametrized L-systems and generalized subdivision for generating complex geometry. In International Journal of Shape Modeling, 2002, vol. 8, no. 2, p. 173-191. Zdroj: BOUDON, F., MEYER, A., GODIN, Ch. 2006. A survey of computer representations of trees for realistic and efficient rendering. Report de recherche. In LIRIS, 2006.

TOMAŠKO, I. 2004. Historické parky a okrasné záhrady na Slovensku. Bratislava : Veda, 2004. ISBN 80-224-0797-6.

trueSpace [online] [cit. 2007-04-12]. Dostupné na internete: <http://www.caligari.com>.

ULAM, S. 1966. Patterns of growth of figures : Mathematical aspects. In KEPES, G. (ed.) Module, Proportion, Symmetry, Rhythm. New York : Braziller, 1966, p. 64-74. Zroj: PRUSINKIEWICZ, P., LINDENMAYER, A. The algorithmic beauty of plants. New York : Springer Verlag, 1990

VAN OYSTAEYEN, F., GIELIS, J., CEULEMANS, R. 1996. Mathematical aspects of plant modeling. In Scripta botanica Belgica, 1996, no. 13, p. 7-27. Zdroj: GIELIS, J. A generic geometric transformation that unifies a wide range of natural and abstract shapes. In American Journal of Botany, 2003, 90 (3), p. 333-338.

VĚTVIČKA, V., MATOUŠOVÁ, V. 1992. Stromy a kry. Bratislava : Príroda, 1992.

ŽÁRA, J., BENEŠ, B., SOCHOR, J. et al. 2004. Moderní počítačová grafika. Brno : Computer Press, 2004. ISBN 80-251-0454-0.

WEBER, J., PENN, J. 1995. Creation and rendering of realistic trees. In SIGGRAPH ’95: Proceedings of the 22th annual conference on Computer graphics and interactive techniques, 1995, p. 119-128.

Spracované podľa:

SMOLEŇOVÁ, K. 2007. Procedurálne modelovanie stromov. Práca k dizertačnej skúške. Bratislava, 2007. 72 p.
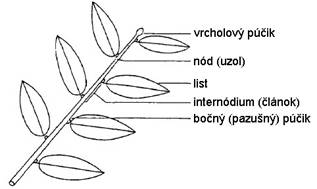
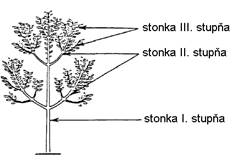
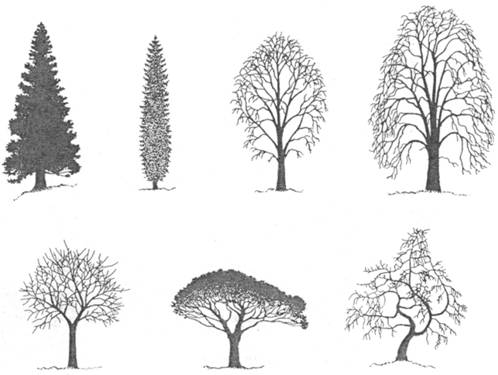
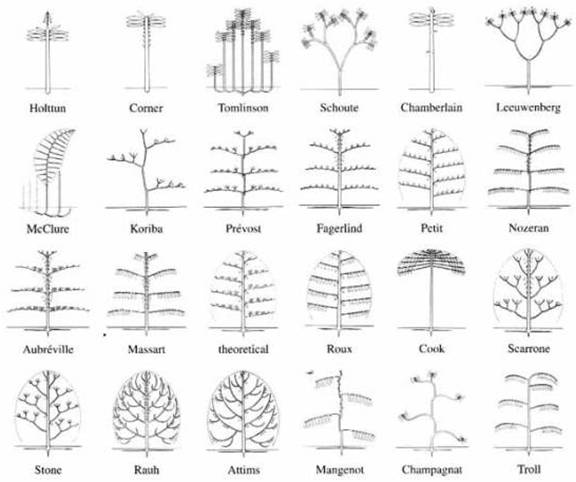
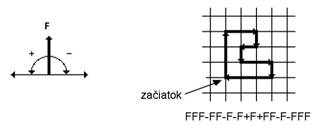
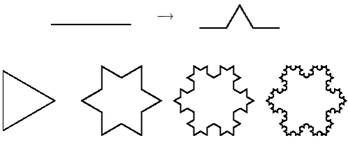
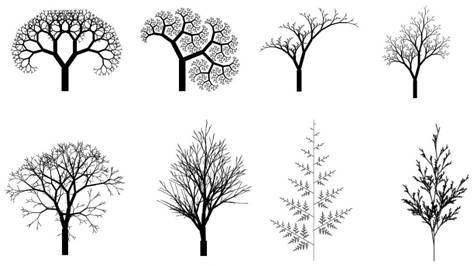