The mutual position of a Bézier curve and regular quadric

Advisor: Assoc. prof. Pavel Chalmovianský, PhD.

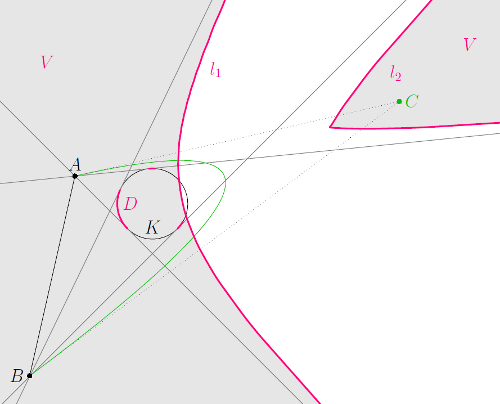
We work in three dimensional space in which a regular quadric is placed. There are two arbitrary points out of quadric. We find a set of all Bézier curves connected these two points such that this path and the regular quadric have no intersection. The spatial problem can be reduced to a planar problem where the the regular quadric is represented by a conic section.

Our method offer a direct computation of all possible collision-free smooth paths without using sample-based planning algorithms. We assume an obstacle represented by regular quadric and given start and end position of robot. We find all quadratic Bézier curves reflect the set of collision-free paths.

There is another use for the affine three dimensional Minkowski space typically determined by a light cone. The points lying outside the cone are called space-like. If we take two space-like points as first and last control points, we can find all quadratic pointwise space-like Bézier curves.